Hypersonic Plane: Waverider

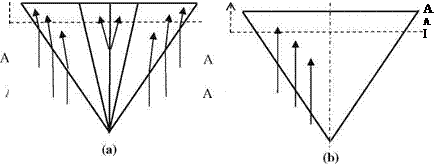
Hitherto, we have seen the various properties of hypersonic flow past different type of body shapes. Now, we can apply this information to analyze the hypersonic aerodynamics of an aerospace plane. The concept of sustainable hypersonic flight of a vehicle having most of the features described in previous sections and riding on the pressure created by the shock surface under its body formally was intro­duced in late 1950s (Nonweiler 1959). In his work, Nonweiler proposes inverted W and V shaped cross sections for delta type wings with surface streamlines and lower surface shocks as shown in Fig. 7.25. The weak shocks appearing at the lower surface create sufficient lower surface pressure so that the lift generated is adequate for a sustainable flight.

This type of aerospace planes which makes use of the lower surface pressure is also called ‘waverider’. According to Nonweiler’s analysis an aerospace plane which was named ‘karet’ then, has stagnation temperature of 1,150°C, at the mid chord region the temperature drops down to 500°C at 80 km altitude with free stream speed of 6.5 km s-1.

Fig. 7.25 Inverted, a W and b V shaped delta wings and shocks and surface streamlines

The waverider concept was quite popular until 1970s, and lost its popularity for some time because of its low lift to drag ratio, L/D. Thanks to numerical opti­mization techniques, towards the end of 1980s, the waverider gained popularity again (Bowcutt et al. 1987; Anderson et al. 1991). In waverider studies, the viscous effects were also considered for the evaluation of optimum (L/D)max for various free stream Mach numbers, at different altitudes and even for planets whose atmospheric properties are known. The previously known (L/D)max barriers were broken with numerical optimization techniques. The free stream Mach number figures given by Kuchemann for 5 M 10, can be improved approximately 1.5. As shown in Fig. 7.26, for a wide range of free stream Mach numbers (2 M 25), Kuchemann’s previously given (L/D)max = 4 (M + 3)/M barrier curve has been changed to (L/D)max = 6 (M + 2)/M because of optimization. Bowcutt et al. even exceed the second curve shown in Fig. 7.26 for M = 20. However, for M = 25 the optimum L/D value is below the given curve. The reason for this behavior is attributed to the Reynolds number effect at high altitudes. The Reynolds number for both free stream Mach numbers is laminar; therefore, for M = 20 viscous drag becomes low to give higher (L/D)max. This gives deviations from the averaged behavior for predicting (L/D)max values.

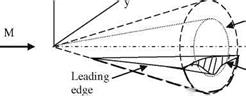
In order to find the optimum shape of a waverider at a given free stream and altitude, first an axially symmetric flow with a weak attached shock of a cone whose angle is the Mach cone angle of the given free stream Mach number is considered (Example 7.3). The leading edges of the waverider are placed inside the conical shock as shown in Fig. 7.27. The upper surface of the waverider is configured as a cylindrical shell surface parallel to free stream. The bottom sur­face, on the other hand, consists of a base curve tangent to the Mach cone surface, and it joins to the leading edge with a bell shaped curve as shown in Fig. 7.27.

After determining the lower surface pressure created by the shock, and the corresponding lifting pressure, we can calculate the total lift by integrating the lifting pressure over the surface. The total drag then is computed by the wave drag induced by the thickness of the wing and the viscous effects. The surface shape

Fig. 7.27 Waverider geome­try placed in shock cone

conical shock surface

which makes the total drag minimum gives us the maximum (L/D) ratio. Calcu­lating viscous drag with reference temperature method, because of its simplicity, is preferred over the boundary layer integral methods (Anderson et al. 1991). The reference temperature method can give the Reynolds number in transition to turbulence based on the free stream Mach number together with the viscous drag in turbulent flow (Anderson et al. 1991).

The waverider shapes based on the ideal flow analysis as given above were also analyzed by solving the Euler Equations (Jones and Dougherty 1992). In that study, the surface pressure distribution is found to be in good agreement with Bowcutt solution and the experimental results for free stream Mach numbers of 4 and 6. In order to find the matching results, a special grid generation based on the adaptive meshing around the sharp leading edges was used.

The optimum shape and the flow field around a waverider was also studied together with Navier-Stokes and Euler solvers results compared (Takashima and Lewis 1994). In their study, Takashima and Lewis found agreement with the surface pressure solution obtained with Navier-Stokes and Euler solvers at free stream Mach number of 6, Fig. 7.28. Here, in that study, the difference between

Fig. 7.28 Upper and lower p / p pressure of a waverider at

2

1.5

y/b

the lower and upper surface pressures gives us the lifting pressure quite similar to that of ideal solution except around the leading edges. While obtaining the viscous solution the flow field is discretized with a fine grid near the surface where the first point above the surface has its y+=0.1 and the sharp leading edge is a little bit smoothed to have a stable solution. The rounding of a leading edge has an effect on the (L/D)max value. It has been observed that if rounding is made with leading edge radius ratio to length of the waverider less than 0.1% then L/D remains constant, if it is larger than 1% than L/D value decreases (Lewis and McRonald 1992).

In their study, Lewis and McRonald extend their work to the aerodynamic analyses of such waveriders which exceed Mach numbers of 50 while passing through the atmosphere of other planets to make use of a gravity assists in their sustainable hypersonic flight.

Approximately 100 km above sea level in the Knudsen number range of 0.05 < Kn < 1 the continuum hypothesis is no longer valid. Therefore, the optimum waverider analysis is made with Monte Carlo method which gives very low L/D ratios (Rault 1994). In his study, based on the Monte Carlo Method, Raul find L/D = 0.197 at 105 km altitude, free stream Mach number of M = 25, and Knudsen number of Kn = 0.05.

The experimental and theoretical work performed so far indicates that towards the end of the first of quarter of twenty-first century, the nations or union of nations with advanced technology will probably start the manned or unmanned sustainable hypersonic flight with prototype waveriders.