Numerical Results

The numerical results include a numerical comparison of the introduced robust for­mulations considering the optimization of a transonic RAE2822 profile under scalar­valued uncertainties. Further, the optimal aerodynamic shape under geometrical un­certainties is computed in a 2d Euler and Navier-Stokes testcase comparing the ad­aptive refinement strategies of sparse grids. The last section shows the influence of shape uncertainties on the quantities of interest in the 3d testcase SFB-401.

7.1 Numerical Comparison of the Introduced Robust Formulations

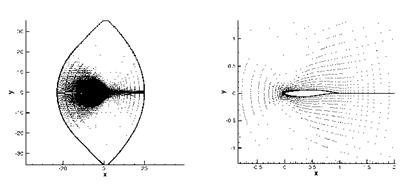
We investigate the shape optimization of a RAE2822 profile in transonic Euler flow, by the use of the CFD software FLOWer provided by DLR within a one-shot frame­work. The block-structured FLOWer code solves the three-dimensional compress­ible Reynolds-averaged Navier-Stokes equation in integral form and provides dif­ferent turbulence models. The equations are solved by a finite-volume method with second order upwind or central space discretization. The discrete equations are in­tegrated explicitly by multistage Runge-Kutta schemes, using local time stepping and multigrid acceleration. In our example, the space is discretized by a 133×33 grid, see Fig. 1. For parametrization, the airfoil is decomposed into thickness and camber distribution. Then, only the camber of the airfoil is parametrized by 21 Hicks-Henne functions and the thickness is not changed during the optimization process.

In this section, we consider the Mach number as an uncertain parameter. The Mach number is assumed to be in the range of [0.7,0.76]. Under the assumption of truncated normally distributed parameter, we obtain the density function shown below in the Fig. 2.

At first, we perform numerical comparisons between a single set-point prob­lem formulation at the setpoint s0 = 0.73Mach with the robust formulations in sections 3.2 and 3.3. In particular, we compare four formulations: (1) non-robust optimization at the Mach number 0.73 (fixed Mach number 0.73), (2) semi-infinite formulation of equations (26-28), (3) chance constraint formulation of equations (34, 35) and (4) non-robust optimization at the Mach number 0.73 (fixed Mach number 0.73) but maintaining feasibility over the whole range of perturbations.

The following figures show evaluations of the objective (drag), Fig. 3, in these cases as well as the constraint (lift), Fig. 4.

We state the following observations: The semi-infinite robust formulation has a better lift to drag ratio than the chance constraint formulation, in particular in

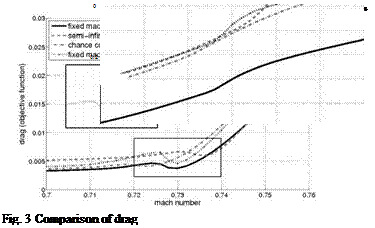
Fig. 4 Comparison of liftconstraint

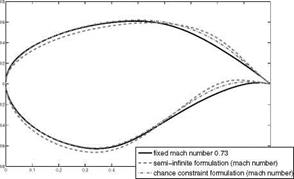
the region above the set-point 0.73, due to the fact that the semi-infinite formula­tion shows a higher lift over the whole range of variations (cf. Fig. 4) and for the greater part a better drag performance than the chance constraint (cf. Fig. 3). Com­paring the robust formulations and the single-set point solution which is feasible over the whole range of variations, the robust solutions leads to a higher drag at the nominal point, but we can observe that the semi-infinite formulation will lead to the best distribution if the Mach number deviates from the set-point. The result­ing shapes are shown in Fig. 5. Summing the results up, it can be stated that the semi-infinite formulations leads to a robust solution which gives a little bit higher drag at the nominal point but a better performance over the whole range of vari­ations. Since the semi-infinite formulation seems to be favorable in our application, the following numerical results considering geometrical uncertainties are based on this formulation.