Numerical Results Considering Geometrical Uncertainties (Testcase RAE2822)
In this section, we present the numerical results of robust optimization under shape uncertainties of a RAE2822 profile in Euler and Navier-Stokes flow. Since the robust optimization problem is solved within a one-shot framework, we use the flow solver TAU provided by DLR which allows the computation of gradients by the adjoint approach in the Euler and Navier-Stokes case. The TAU Code is a CFD software package for the prediction of viscous and inviscid flows about complex geometries from the low subsonic to the hypersonic flow regime employing hybrid unstructured grids. In the Euler case, the profile is described by 129 surface grid points and in the Navier-Stokes case, by 192 surface grid points. Again, the airfoil is parametrized by 21 Hicks-Henne functions. The geometry uncertainties are characterized by a Gaussian random field and the following second order statistics
E(у(х, Z)) = 0 Ух є Г (72)
Cov(x, y) = (0.005)2 • exp (-J^£) Vx, y є Г. (73)
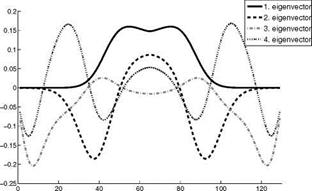
One realization of the random field and the resulting perturbed geometry is shown in Fig. 6 and Fig. 7. Representing the random field for the numerical treatment у in a finite number of independent random variables using the Karhunen-Loeve – Expansion, one has to solve the eigenvalue problem (9). In our two-dimensional testcase, the discretization of the profile leads to a matrix of size (129 x 129) and (192 x 192) in the Navier-Stokes case, so the eigenvalues and eigenvectors can be computed by common methods. The distribution of the eigenvalues of the given random field (72-73) is shown in the next Fig. 8. As stated before, the eigenvalues exponentially converge towards 0. For the first numerical results, we have considered only the first four eigenvalues and eigenvectors to represent the random field у of
|
|
|
Fig. 6 One realization of the random field perturbations on the upper side of the profile (above) and on the lower side (below) |
|
Fig. 7 Resulting perturbed geometry compared with the original shape (dashed line) |
perturbations. The corresponding eigenvectors are shown in Fig. 9 Using the truncated Karhunen-Loeve representation, the mean value of the drag is then computed by
The random variables Yi are uncorrelated and therefore independent, so one has to approximate a four-dimensional integral in the optimization problem. To further reduce the computational effort, we investigate the influence of the individual eigenvectors in order to reject those eigenvectors from the reduced basis which have no impact on the target functional. Since the following results are problem dependent, we will now distinguish the Euler and Navier-Stokes case.
|
|||||
|
|||||
|
|||||
|
|
||||
|
|
|
|||
|
![]()
Fig. 9 First four eigenvectors of the given random field у