Phugoid

The phugoid mode is a lightly damped low-frequency oscillation. The aircraft responses in phugoid are very slow compared to the changes in the motion parameters in SP mode. Chapter 7 shows a time history plot for the phugoid mode. This mode describes the long-term translatory motions of the vehicle center of mass with prac­tically no change in the angle of attack. This mode involves fairly large oscillatory changes in forward speed, pitch angle U, and altitude h at constant angle of attack.

An approximation to phugoid mode can be made by omitting the pitching moment equation:

(5.20)

where g is the acceleration due to gravity.

Forming the characteristic equation and solving for the eigenvalues yields the following expressions for the phugoid natural frequency and damping ratio:

Zug щ
Frequency	(5.21)

Xu

2wnph

Example 5.4

The aerodynamic derivatives of a transport aircraft in phugoid mode are given as Xu — —0.015, Zu — —0.1, u0 — 60 m/s

Use the phugoid model of Equation 5.20 and obtain the frequency responses and other characteristics.

Solution

The state-space model is written as

u		—0.015	—g	u		0.01
u	—	0.1 60	0	U	+	0

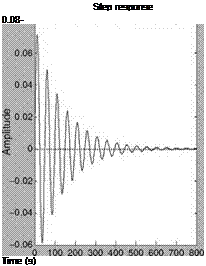
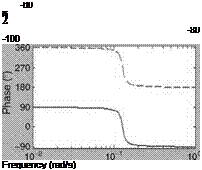
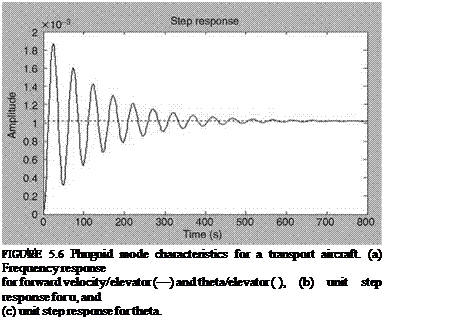
Based on the procedure of the previous examples, the TFs and the frequency responses are obtained for this phugoid model. The natural frequency of this mode is 0.128 rad/s and the damping ratio is 0.0587. The frequency and unit step responses are shown in Figure 5.6. Since the damping ratio of this mode is very small, the oscillations last for several seconds. Since the amplitudes are small and oscillations are of low frequency, the pilot would be able to manage these oscillations very well.

There is a possibility of a 3DOF phugoid approximation model. This can be done by retaining the derivatives related to the vertical speed:

(s — Xu)u — Xww + gU — XSe Se —Zuu + (s — Zw) w — Uos6 — ZSe8e —Muu — Mww — MSe 8e

With

Generally the phugoid frequency and damping increase in proportion to Mu.

In summary, we see that free longitudinal motions of the aircraft comprise of two oscillatory mode characteristics. This means that the forward velocity to elevator amplitude/magnitude (of the TF) will be much smaller at the natural frequency of the SP compared to that at the phugoid frequency. The phugoid mode will not have any change in the angle of attack. The higher vertical acceleration has a pronounced effect on the altitude and its rate of change. In general, irrespective of the size and weight of an aircraft, its basic characteristics can be described in a very simple manner in terms of only a few parameters, say two or four aerodynamic derivatives. This is made possible because a linear system is applicable to simplified dynamics and the related TF/control system concepts.

Bode diagram
0
-20 TS
-40
(a)
(b)