Prandtl Lifting Line Theory

15.10.2.1 Lifting Line Theory

The downwash results from the presence of a vortex sheet, downstream of the sharp trailing edge of a finite wing. The sheet is made of line vortices which induce a negative vertical velocity component when the lift is positive, as required from a balance of momentum.

Downwash is associated with induced drag, whereas upwash will produce thrust (negative drag).

There is no net drag benefit to design a wing with upwash. The wing with minimum induced drag for a given lift has elliptic circulation and constant downwash. Any other induced velocity distribution, including with upwash, will produce more induced drag.

15.10.2.2 Design of a Wing

The circulation distribution is represented by the Fourier series

■ Г[y(t)] = 2Ub Z“=1 An sin nt
y(t) = -§ cos t, 0 < t < n

Combining modes 1 and 3 and taking the derivative w. r.t. t yields

2Ub (A1 cos t + 3A3 cos 3t) = 0, at t = 0 and n

requiring

A1 + 3 A3 = 0

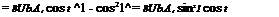
Using the identity: cos 3t = cos t 4 cos2 t – 3 one finds d Г [ y (t)]

dt

and the derivative w. r.t. y reads

The requirement is satisfied for zero strength tip vortices. With this choice, the circulation distribution becomes

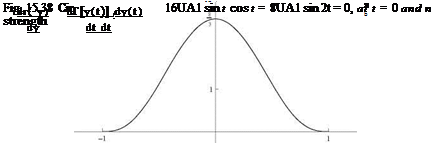
where we used the identity: sin 3t = sin t (4 cos21 — 1). The circulation distribution Г[y(t)] is shown in Fig. 15.38.