RATE OF DESCENT IN VERTICAL AUTOROTATION

Even though vertical autorotation occurs in the vortex ring state, a first approximation procedure for calculating the rate of descent may be derived from a combination of blade element and momentum concepts. Setting the torque equation for the ideally twisted rotor to zero gives:

2 2	4

FIGURE 2.11 Effect of Main Rotor Wake and Direction of Tail Rotor Rotation at Yaw Trim Conditions

Source: Yeager, Young, & Mantay, “A Wind-Tunnel Investigation of Parameters Affecting Helicopter Directional Control at Low Speeds in Ground Effect,” NACA TND-7694, 1974.

-50 -45 -40 -35 -30 -25 -20 -15 -10 -5 0 FIGURE 2.12 Pedal Activity in Left Sideward Flight of Hughes AH-64

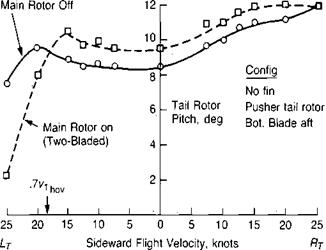
Sideward Speed, knots

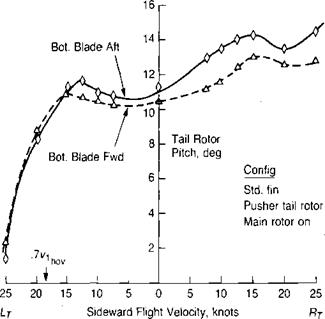
Source: Prouty, “Development of the Empennage Configuration of the YAH-64 Advanced Attack Helicopter," USAAVRADCOM TR-82-D-22, 1983.

where from the hovering derivation:

(0r — фг) = CT ——

The inflow angle at the tip, фт, is:

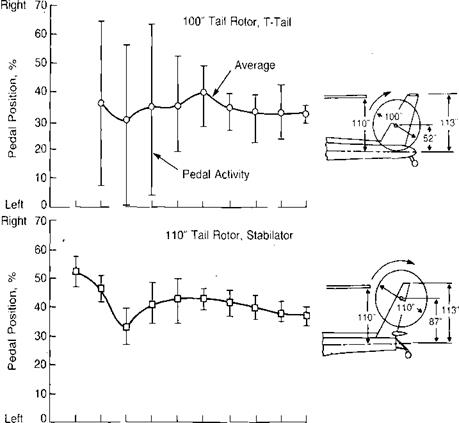
Source: Castles & Gray, “Empirical Relation between Induced Velocity, Thrust, and Rate of Descent of a Helicopter Rotor as Determined by Wind-Tunnel Tests of Four Model Rotors,” NACA TN 2474, 1951.

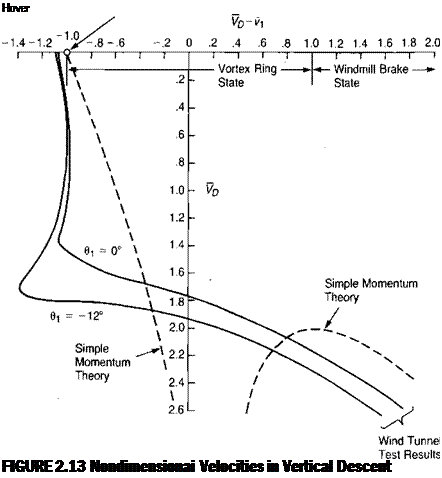
This result is so typical that a rule of thumb is that the rate of descent in vertical autorotation is twice the hover-induced velocity. This is also borne out by an examination of Figure 2.8. Figure 2.13 shows that an untwisted rotor is better than a twisted one for vertical autorotation in that a lower rate of descent is required.

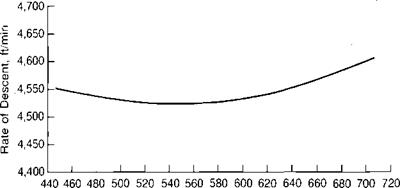
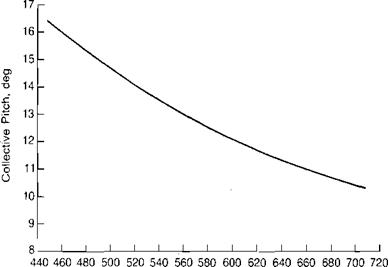
The rate of descent is a function of rotor speed; the minimum ocurring at the rotor speed that corresponds to the maximum c,/2/q. Figure 2.14 shows the calculated rate of descent of the example helicopter as a function of rotor speed. The minimum rate of descent occurs at a tip speed of about 550 ft/sec. Although this represents a theoretical optimum, it is not a practical condition since the rotor is on the verge of blade stall, which could be triggered by small changes in flight conditions, and because of the relatively low value of kinetic energy stored in the rotor for use in the landing flare. It is more likely that the pilot would try to hold

Tip Speed, ft/sec

Tip Speed, ft/sec FIGURE 2.14 Effect of Tip Speed on Rate of Descent in Vertical Autorotation

the normal power-on tip speed or even a value slightly higher. The collective pitch required as a function of tip speed can be estimated by combining equations already derived.

3 3

0O = — 0T –0, 0 2 ^Idcal twist ^ 1

For these calculations, no power losses due to the transmission, accessories, or tail rotor have been considered. For actual cases where the rotor must supply the extra power, Ah. p., the equation for the velocities becomes:

	1 ( 4,400Ah. p.
	P Ab^ClRycd_

For the example helicopter, it is estimated that the rotor must develop 40 hp during vertical autorotation. This will increase the value of (VD — by 11%, but the rate of descent will increase by only 1.5%. It is of some interest to note that the rate of descent of a parachute is given by the equation:

For a parachute with the same disc loading as the example helicopter and a drag coefficient of 1.2, the rate of descent is 4,260 ft/min—approximately the same as the helicopter. This comparison adds validity to the observation that the rate of descent of the helicopter in autorotation is approximately twice the hover – induced velocity. (A parachute with a drag coefficient of 1.0 would be an exact analogy of the helicopter in this condition.)