TBL excitation

The response and sound radiation of the panel when it is excited by the fully developed TBL pressure field is finally studied with reference to the spectra of the total kinetic energy PSD and total sound power radiated PSD shown in plots (g) and (h) of Figure 11. At low frequencies, the spectrum of the kinetic energy PSD is similar to that for the panel excited by the uncorrelated pressure field shown in plot (e). In fact, the response is characterised by well separated sharp resonance peaks of all natural modes with either odd or even mode orders. However, in contrast to what found with the ROR excitation, in this case the amplitude of the resonance peaks is uneven. These effects are produced by two concomitant properties of the TBL excitation. On one hand, as seen for the ROR excitation, the TBL pressure field is composed by a stochastic distribution of small patches of transverse force excitations that couples efficiently with all modes of the panel. On the other hand, the convected fluid tends to smear these excitations in a waved pattern along the stram-wise direction. Thus the coupling of the waved excitation field with the resonant modes varies depending on the plate mode order in the direction of the fluid flow. At about 1.17 kHz, the spectrum of the response PSD shows a small ridge, which is due to the so called “convective coincidence” or “aerodynamic coincidence” effect. As discussed in Chapter 6, the vortexes that develop in the TBL fluid flow are conveyed in the stream-wise direction at the convective velocity Uc. Thus the pressure field generated over the panel is characterised by an exponentially decaying correlation function in span-wise direction and a weaved exponentially decaying correlation function in stream-wise direction, whose characteristic wave length is given by Xc = 2^/kc, where kc = co/Uc is the convective wave number. As a

result, the panel is efficiently excited at frequencies close to the so called “convective coincidence frequency”, where the wavelength of the flexural vibration in the flow direction coincides with the correlation wavelength that characterises the TBL pressure field in the stream-wise direction, i. e. =XC. This condition implies that kb = kc and thus, considering that

kb =^cb =4a{mpjBp and kc = a/Uc, the convective coincidence frequency can be readily derived as follows:

This expression suggests that the convective coincidence frequency grows with the square of the convective speed Uc. Recalling that the convective speed is a

fraction of the flow velocity, i. e. Uc = KUm with 0.6 <K<0.85 and comparing

Eq. (83) and Eq. (82) for the lower acoustic coincidence frequency, it is noted that

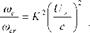(84)

Thus, even for a sonic speed of the flow, i. e. Um – c, the convective coincidence frequency is 1.4 to 2.8times smaller than the critical frequency. When the speed of the flow is lower than the speed of sound, the convective coincidence frequency becomes much smaller than the lowest acoustic coincidence frequency. Thus, for most vehicles, the convective coincidence effect is likely to occur in the low to mid audio frequency range where noise is mostly perceived as a source of annoyance and, as will be discussed in the next section, passive sound insulation treatments are less effective. Indeed, as can be noted in plot (g), the spectrum of the kinetic energy is characterised by a wide band ridge around the convective coincidence frequency that, as highlighted by the thick-solid vertical line, for the panel and flow conditions at hand, occurs around 1.17 kHz. As seen for the acoustic coincidence phenomenon, the convective coincidence can also be analysed in terms of dispersion curves for the flexural wave and for the fluid-dynamic convective effect. As an example, Figure 12 shows the dispersion curves for the plate flexural wave and for the TBL fluid flow considered in this study. The two curves intersect at kb = kc, that is at the convective critical frequency a>c.

Moving back to the analysis of plot (g), at frequencies above the convective coincidence frequency, which is highlighted by the thick-solid vertical line, the spectrum of the kinetic energy becomes increasingly smoother, since the response of the panel at each frequency is due to the overlap of an increasing larger number of modes. As a result, the spectrum is characterised by wide frequency band crests with multiple resonant modes, spaced out by wide frequency band troughs. The spectrum of the kinetic energy falls rapidly with a 12 dB / octave slope, thus following the so called “stiffness law”, since the response is controlled by the stiffness of the panel. The spectrum continues to fall rapidly even at very high frequencies around acoustic coincidence.

Considering now the sound power radiated, by contrasting plots (h) and (f), it is noted that, below and around the convective coincidence frequency, which is highlighted by the thick-solid vertical line, the spectrum of the radiated sound power generated by the TBL excitation is quite similar to that produced by the ROR excitation, although the spectrum in plot (h) shows a much uneven sequence of resonance peaks. This is due to two phenomena. Firstly, as discussed above, the convected stochastic excitation field couples with all modes but
unevenly. Secondly, at frequencies below the acoustic critical frequency, the sound radiation efficiency varies from mode to mode. As seen for the kinetic energy in plot (g), at frequencies above the convective coincidence frequency, the spectrum of the radiated sound power in plot (h) becomes increasingly smoother, since the response of the structure is given by the overlap of an increasingly larger number of modes. Similarly to the spectra obtained for acoustic excitations in plots (b) and (d), the mean value of the spectrum in plot (h) tends to fall with a 6 dB / octave slope up to higher frequencies around the acoustic coincidence frequency, where the spectrum shows the characteristic wide band ridge with multiple resonance peaks due to the enhanced sound radiation properties of all modes. At further higher frequencies, the spectrum resumes the 6 dB / octave slope.