The Main Assumption

We now emphasize a key assumption made in deriving all of these important results: The flow field is incompressible; density variations are ignored. This asumption may not seem important until we realize that it leads to strict limitations in the domain of applicability of the results herein, especially in terms of speed range of an aero­dynamic vehicle. We put these limitations in perspective by examining the speeds of various common flight vehicles with the object of determining which classes of vehicles are governed by the analyses carried out to this point.

We show in previous chapters that aerodynamic performance often can be described in terms of the cost in drag associated with the production of lift. Lift is the main output of the aerodynamic system and it is used directly in countering gravitational forces, thereby rendering atmospheric flight possible. We demon­strate in Chapter 1 that a useful figure-of-merit for aerodynamic performance is the L/D ratio.

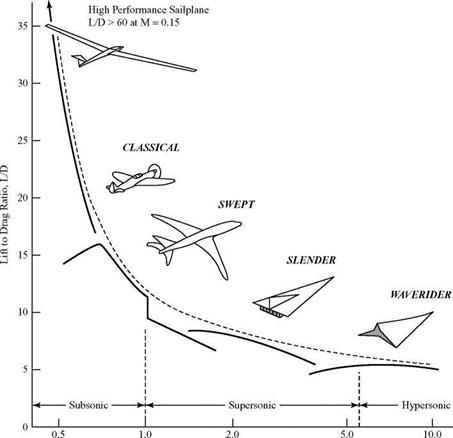
Consider the effect of speed on the achievable L/D ratio by an optimally designed flight vehicle. Figure 9.1 is a typical presentation of such information. The horizontal axis covers speeds from the lowest possible (corresponding perhaps to a man-powered aircraft) to the highest velocities for atmospheric flight vehicles that may nearly reach the speed required for earth orbit. The Mach number (i. e., dimensionless speed) is used to reflect the velocity on the horizontal axis because it directly reflects the importance of compressibility.

Several useful observations should be apparent on inspection of Fig. 9.1. The first is that there is a definite optimal aerodynamic configuration associated with each speed range. We classify those in the manner suggested by Kuchemann. It may be disappointing to see that all of our labors are applicable only in the lower part of the subsonic speed range (i. e., to “classical” airplane configurations) and appropriate only in the speed range up to approximately 400 mph (640 km/hr). We refer to this as the speed range for the classical aircraft-design configuration because, indeed, it is the earliest and most common type and still absorbs a major effort by aircraft designers.

For emphasis, it is crucial to understand that the aerodynamic models devel­oped thus far apply only to low speeds (i. e., up to about 600 km/hr)—that is, to flight Mach numbers less than, say, 0.6. The aerodynamic performance of a classical airplane shape falls off drastically at higher speeds, and it may not even be capable of stable flight due to shifting of the center of pressure as compressibility effects become important. It is clear, then, that there is much to accomplish if we are to understand the design process for high-speed aircraft. Fortunately, as demonstrated for the low-speed range, there exists a multitude of powerful simplifying assump­tions and “ingenious abstractions and approximations” of the type we already use up to this point for incompressible flows.

It remains to explain in more detail how we can use what we have learned in the pre­diction of performance and in the practical analysis and design of efficient, classical flight vehicles. Many of these applications of aerodynamics qualify for textbooks in their own right; therefore, only an introduction is possible here. The subjects of vehicle performance, stability and control, and so on, most often are treated in separate courses. Students will find in their study of those subjects that a thorough understanding of the aerodynamic principles examined herein is indispensable. Stu­dents may find it useful as we start this discussion to review Chapter 1 to examine the photographs and descriptions of classical subsonic aircraft.