WAVERIDER AIRCRAFT

8.1 The waverider concept and its possible applications. We shall now dis­cuss the aerodynamics of a type of aircraft which as yet exists only in our minds. The technology for building it has not yet been developed. Therefore, we cannot carry out a simple performance analysis, as we did before with other types of aircraft, to determine the types of flow and the kind of aircraft shape we should investigate before going into details. We must find some other criteria to direct us towards some definite aims. This lead can be provided by the social motivation of aviation and by some fundamental know­ledge in fluid mechanics, which has been worked out during the last century.

We have already pointed out in Chapter 1.3 (see also P L Roe (1972)) that, in all the history of travel, we may observe two constants which, because they concern human nature, may confidently be extrapolated into the future. One of these is the significance of personal contact between people, and the other is the reluctance of most people to undertake frequently journeys which last for more than a few hours. Regardless of how any of us personally regards the prospect of a "global village" in which all men are members of a truly inter­national society, it does seem very probable that this is the eventual destiny that a peaceful earth must tend toward. But this cannot come about until all major cities and centres of population are brought within a few hours of each other: the means of travel must grow to embrace the globe. To do this in a way which suits human nature is the contribution that aviation can make, and this must be our ultimate aim.

Following P L Roe (1972), we may think in terms of regions which will have to be brought within reach of convenient travel. We may suppose that the number of journeys people will wish to make from one region to another depends in some way on the number of "attractions" to be found in the other region, such as trading centres, political capitals, mineral wealth, holiday resorts, or just "people" and "places" they would like to meet and to see. If we suppose that the attractiveness of a region is simply proportional to its area, then the requirement for journeys over a distance R is

J(R) = sin (irR/R ) , (8.1)

g

for a spherical earth, where Rg = 20000km is the "global range". Very roughly, the actual distribution of population in large cities, shown in Fig.

1.5, looks like that, with a secondary peak at short ranges in the already developed regions and a maximum for the potentially most heavily used trans­port routes at about one quarter of the way around the globe. This is a striking enough conclusion, and we may expect that the actual transport requirement will, in time, approach something like that given by (8.1).

If we now add the condition that the journey time should not exceed about 2 hours, say, we find that the existing types of aircraft, which we have dis­cussed so far, cannot do the job. A slender aircraft flying at Мд m 2 would take more than twice that time to get one quarter of the way around the globe, and a high-subsonic swept-winged aircraft would take 8 to 10 hours or

more (see (1.13)). What we are looking for, therefore, is an aircraft that can fly at least at a Mach number between 4 and 5 and can speed up to Mach numbers between 8 and 12, say, to cover the full global range in good time. This, then, gives us a starting point: we cannot be satisfied with the types of aircraft we have got – we have to think out and develop at least one further type, if we take our responsibilities towards probable long-term transport needs seriously.

But could existing types of aircraft even achieve half a global range? The estimates given in Fig. 1.3 indicate: yes, but only just. We can now supplement these results by applying the aerodynamics of swept and of slender aircraft derived in previous chapters in a way which will give us some overall view of the comparative capabilities of these types of aircraft and, at the same time, chart out where we should look for a new type. To do this

in a simple way, we use the Br£guet equation (1.7) for the range and assume

some modest values on present technology for the combined propulsive aero­dynamic efficiency TipL/D such as ЛрЬ/D «3 at Mq = 2 for swept aircraft, in accordance with the results in Fig. 4.9. We also assume that aircraft can be designed to have a reasonable payload fraction when the fuel fraction is Wf/W ■ 0.45 and when the fuel is kerosene. As before (see e. g. Fig. 4.76), we describe the geometry of the aircraft simply by the box size, s/I, into

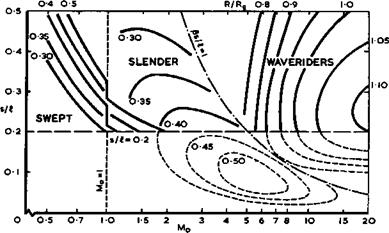
which it can be fitted. In a diagram with s/i and Mq as axes as in Fig.

8.1, lines along which R/Rg reaches certain values can then be drawn. This diagram can be subdivided into regions by three other lines which have some aerodynamic significance: a line along s/fi – 0.2 is meant to indicate that aircraft below it will be inadequate on the airfield; a line at Mo “ 1 indicates sonic speed but has no longer the significance of a "barrier"; a line along which $s/& ■ 1 indicates where a delta wing has a nominally sonio teading edget which has a greater general significance. The results in Fig, 8.1 show that the main regions of application of swept and of slender aircraft fall quite neatly into the sub-divisions of the diagram. Swept air­craft could achieve R/Rg = 0.5 but would take too long a flight time. If we impose a time limit, then we should regard high-subsonic or low-supersonic

Fig. 8.1 BrAguet ranges for various types of aircraft

LIVE GRAPH

Click here to view

swept aircraft as best suited for ranges up to between 2000km and 3000km; a range of about 5000km could be achieved in good time if we could entertain the idea of designing a swept aircraft to fly at Mq = 2 . Slender aircraft cannot quite achieve R/Rg =0.5 ; their peak turns out to lie underneath the "groundline" s/l = 0.2 , as it were, and only the application of powered lift on a big scale, as originally proposed by A A Griffith (1954, unpub­lished), could make this realisable in aircraft. Slender wings are obviously best suited for transatlantic and intercontinental ranges at Mach numbers around 2. All these existing types of aircraft lie clearly to the left of the line gs/H. = 1 .

This leads us to search for a new type of aircraft in the region to the right of the line &s/l = 1 and above the line s/l = 0.2 , and this, in turn, must bring in a new type of flow. Any aircraft shapes in that region can no longer cause only small disturbances in the air; we must now consider shapes which produce strong shockuaves in the flowfield and find means for applying these usefully. We can expect that these strong disturbances will be caused by the means for generating lift and also by the means for providing volume and propulsion. P L Roe (1972) has developed a line of basic arguments which leads to the conclusion that the part of the aircraft that provides volume should be integrated with the propulsion system and also with the lifting system, i. e. we should deal with the concept of an aerodynamically integrated propulsive lifting body. This implies that the flowfields to be considered represent the combined effects of all three means together, not the super­position of various effects of separate means with an essentially small amount of "interference" between them.

Another condition, which we are not prepared to renounce, is that the new type of aircraft should be able to fly well at low speeds and be capable of taking-off and landing, preferably without a change in its geometry. We know of only two types of flow which will allow this: one is the classical aero­foil flow, and the associated shapes are clearly unsuitable for flight in the Mach number range envisaged; the other is the slender-wing flow, and in this

case we can expect that the associated shapes might be suitable. We may,

therefore, try to find shapes which behave at low speeds like the slender wings we already know. Thus we can state at once that we want to consider shapes with aerodynamically sharp edges and near-triangular planform with a semispan-to-length ratio of about 1/4 (i. e. not below about 1/5 and not above about 1/2). In cruising flight, the leading edges will be nominally super­sonic, as defined in section 6.3, equation (6.37).

These general features imply that we do not expect to find shapes which can have the same type of flow throughout the whole flight range. The aircraft with a given value of s/i will have to pass the lines Mq = 1 and

6s/A = 1 and back again. This change in the type of flow is an important

departure from previous practice, and we must prepare ourselves to cope with such changes. We can at least demand from the outset that they should be gradual and controllable.

We have already discussed in general terms how lift can be generated at high Mach numbers by a thick body (see section 3.4, Fig. 3.9) and how thrust can be generated in flow cycles with heat addition (see section 3.6, Fig. 3.16).

We have also indicated that liquid hydrogen might be a suitable fuel for high-speed flight (see Chapter 1.2), and we assume now that this will be applied. These elements can then be combined to derive a complete aircraft. The shapes to be considered are described by the generic term "waverider" because at some design condition, a shockwave may be contained between the leading edges below the body. Anticipating results to be derived below, we can draw some lines in Fig. 8.1 for ranges which may be achieved by wave- riders, again on the assumption that an aircraft with reasonable payload can be constructed when the fuel fraction Wp/W =0.45 . Such estimates may not be very reliable, at the present state of knowledge, but they can give us a first overall view and a crude map of what lies before us (see e. g.

D KUchemann (1965), J Seddon and A Spence (1968), D Ktlchemann & J Weber

(1968) ).

The estimates in Fig. 8.1 show that the waverider aircraft of interest, which we should investigate further, all lie sensibly to the right of the line gs/£ = 1 . These shapes are aerodynamically non-slender and they are thus quite distinct from the others. The new aerodynamics and the use of hydrogen fuel dramatically increase the range beyond that of existing types of air­craft, to cover half to full global ranges within the time limit we set our­selves. This implies that the flight Mach numbers of interest lie between about 4 and about 12. It does not seem worthwhile to go further and faster.

A more detailed analysis by D H Feckham & L F Crabtree (1967) has come to the same general conclusions. They assumed a more realistic flight path, with a climb at a constant acceleration of 0.2g, then a cruise phase at a constant Mach number, and finally descent along a glide path. For the ranges and Mach numbers considered here, they find that there is a substantial phase of cruising flight within the atmosphere left, i. e. we are dealing with an ordinary aircraft again, not with a boost-glide vehicle which does not cruise and might leave the atmosphere. This distinguishes the waverider aircraft to be discussed also from any of the various space vehicles, although, as it happens, the shapes to be considered may also be suitable for space shuttle orbiters, as shown by L H Townend (1972) (see also L C Squire (1975)).

This restriction to aircraft flying in the atmosphere at Mach numbers below about 12 allows us to leave aside, on the whole, any matters associated with rarefied gasdynamics or real-gas effects in flows (for a discussion of condi­tions when such effects may arise, see e. g. W Wuest (1970), (1973), and

(1975) ). We shall be concerned again with continuum gasdynamics in the ordinary sense and discuss inviscid compressible flows as well as some vis­cous interactions, but not the chemical reactions which go together with heat addition to air flows. Thus, even though we deal with a hypothetical new type of aircraft, we can build on much basic knowledge which has been avail­able for a long time and apply results which have been found by men like W J M Rankine (1870), E Mach & P Salcher (1887), H Hugoniot (1885) (1887) (1889), D L Chapman (1899), E Jouguet (1905) (1906), L Prandtl (1907), and Th Meyer (1908). A possible waverider aircraft may bring their work to some technological application. This means that, strictly, we are concerned with supersonic flows past bodies which cause strong perturbations, where the air can be treated as a continuum substance in thermodynamic equilibrium. Some use the term hypersonic to describe such high-speed flows, and the waveriders to be discussed would then be hypersonic aircraft.

The aerodynamic background information we need to deal with these flows can be found in many textbooks, and we mention here those by R Courant &

К 0 Friedrichs (1948) H W Liepmann & A Roshko (1957), R N Cox & L F Crabtree

(1965) , and W D Hayes & R F Probstein (1966).