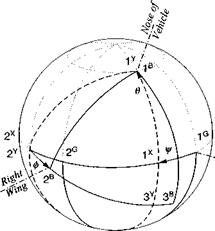
Body coordinate system

The preferred body coordinate system is aligned with the body triad of Fig. 3.7. The Iя axis points through the nose of the vehicle and lies with the downward-pointing 3B axis in the plane of symmetry. The 2B axis, out the right wing, completes the coordinate system.

A prominent transformation matrix in flight mechanics is the TM of body coor­dinates wrt geographic coordinates TBG. It is composed of three transformations by the so-called Euler angles: yaw, pitch, and roll or ф, в, and ф. Two intermediate systems ]x and ]y are needed to complete the chain:

[T]BG = [Г(0)]ЯУ[Г(0)]га[Г(^)]хс

As Fig. 3.16 shows, the unit sphere is getting more cluttered, and you should be grateful for the orange peel rendering, showing only the essentials without coordinate axes jumbling up the picture.

Let us start the chain reaction with the geographic ]G to the first intermediate ]x system through the yaw angle i/r. The transformation occurs about the 3G axis.

Therefore we have the pattern
cos ф sin ф 0 [T]XG = —si пф cos ф 0 0 0 1
The second transformation is about the 2X axis through the pitch angle # to the second intermediate system ]y:
1 0 0 [T]BY = 0 cos ф sin ф 0 —sin ф cos ф
Now it is just a matter of multiplying the three matrices to obtain the Euler trans­formation matrix:
cos ф cos 9 [Т]вс= cos ф sin 9 sin ф — sin ф cos ф cos ф sin 9 cos ф + sin ф sin ф
sin ф cos 9 sin ф sin 9 sin ф + cos ф cos ф sin ф sin 9 cos ф — cos ф sin ф	—sin# cos 9 sin ф cos 9 cos ф
# = arcsin(—0з) and from the elements t\ and t2 the yaw angle
(3.15)
ф = arctan and lastly from the elements ь3 and t33 the roll angle
(3.16)
ф = arctan
(3.17)

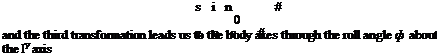If you change the sequence of the matrices, you do not get the same transfor­mation matrix because matrix multiplications do not commute. However, because matrix multiplications are associative, you can change the order of the multipli­cations without changing the result. Convince yourself of these facts by using the matrices of this example.