Channel Flow in a Compressible Fluid

In three-dimensional, compressible, isentropic flow, the following relation­ships can be shown to hold (see Ashley and Landahl [161]):

• Equation of fluid motion

where ф is the velocity potential of relative fluid motion related to the per­turbed velocity potential cp through the equation

ф = – x + (p,

as and aSo are, respectively, the local velocity of sound and the velocity of sound at upstream infinity, M0 = U0/aSo is the Mach number in the unper­turbed oncoming flow, and 7 is the ratio of the specific heat of gas (isentropic parameter); for air, 7 = 1.4;

Excluding (as/aSo)2 from (5.1), we can derive the following equation to de­termine the relative velocity potential:

_M°2 Ш + !(w)2 + ‘ V(W)21= °- (5-4)

In the channel flow region D, we introduce stretching of the vertical coordi­nate у — у jh and seek ф in the form of an asymptotic expansion

(5.5)

where

{ФІ, ФГ) = 0(1), Фї = фн + Ь1п^фІ2 + 1гф1з. (5.6)

Passing over to the channel flow variables and accounting for the adopted asymptotics (5.5) of the potential in the gap between the lifting surface and the ground, we obtain the following relationships with respect to the potential function ф*:

• Continuity equation:	д2ФЇ (Щ2 n. dy2 V dy J ’	(5.7)
• Boundary conditions:
дф* dy	= 0 for у = yi and у = yg.	(5.8)
A solution, satisfying both (5.7) and (5.8), has the form
	Ф = Ф(х>2)-	(5.9)

The corresponding equation for (5.6) and (5.9): d2ф** _ dy2

ф** can be obtained by taking into account

where Л/і,2 are nonlinear differential operators in the two variables x and г:

i(7-l)M2[l-[V2( )]2-2^]}a2{ ),	(5.11)
w) + >’< )l! + 5V2()’v’iv< >p]	ч	(5.12)
. _2 _ . 0 f d ^2 = V2, V2 = г— + fc —.		(5.13)

ал*- Ж.

-л* м2

Integrating (5.10) once with respect to у and using the flow tangency condi­tions for ф** identical to (2.15) and (2.17), where </?** — x should be replaced by </>**, we obtain the following channel flow equation for compressible isen- tropic flow (Rozhdestvensky [41]):

h* = h*/h, /г* = h*(x, z,t) is a prescribed instantaneous gap distribution. To solve the lowest order problem (the extreme ground effect), one has to replace ф* by фг and apply the following boundary conditions at the planform contour:

(fx = x + фг =0 at the leading edge, (5.15)

рг = 0 at the trailing edge. (5.16)

Inspecting the expression for the pressure coefficient in compressible flow, (see Ashley and Landahl [161]),

To satisfy (5.16) for compressible case, it is sufficient to require that

For small perturbations, linearization of equation (5.14) leads to the following lowest order problem with respect to the perturbed velocity potential :

<9×2 <9z2

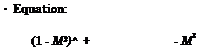
• Boundary conditions at the planform contour:

(рг =0 at the leading edge, (5.20)

Ph — 2 f-гг1 – =0 at the trailing edge. (5.21)

ox ot )