Compliant walls: artificial dolphin skins
It is widely thought that some dolphin species possess an extraordinary laminar-flow capability. Certainly mankind has long admired the swimming skills of these fleet creatures. Scientific interest in dolphin hydrodynamics dates back at least as far as 1936 when Gray^ published his analysis of dolphin energetics. It is widely accepted that species like the bottle-nosed dolphin (Tursiops truncatus) can maintain a sustained swimming speed of up to 9 m/s. Gray followed the usual practice of marine engineers in modelling the dolphin’s body as a one-sided flat plate of length 2 m. The corresponding value of Reynolds number based on overall body length was about 20 x 106. Even in a very-low-noise flow environment the Reynolds number, Rext, for transition from laminar to turbulent flow does not exceed 2 to 3 x 106 for flow over a flat plate. Accordingly, Gray assumed that if conventional hydrodynamics were involved, the flow would be mostly turbulent and the dolphin would experience a large drag force. So large, in fact, that at 9 m/s its muscles would have to dehver about seven times more power per unit mass than any other mammalian muscle. This led him and others to argue that the dolphin must be capable of maintaining laminar flow by some extraordinary means. This hypothesis has come to be known as Gray’s Paradox.
Little in detail was known about laminar-turbulent transition in 1936 and Gray would have been unaware of the effects of the streamwise pressure gradient along the boundary layer (see Section 7.9). We now know that transition is delayed in favourable pressure gradients and promoted in adverse ones. Thus, for the dolphin, the transition point would be expected to occur near the point of minimum pressure. For Tursiops truncatus this occurs about half way along the body corresponding to Rext = 10 x 10°. When this is taken into account the estimated drag is very much less and the required power output from the muscles only exceeds the mammalian norm by no more than a factor of two. There is also some recent evidence that dolphin muscle is capable of a higher output. So on re-examination of Gray’s paradox there is now much less of an anomaly to explain. Nevertheless, the dolphin may still find advantage in a laminar-flow capability. Moreover, there is ample evidence which will be briefly reviewed below, that the use of properly designed, passive, artificial dolphin skins, i. e. compliant walls, can maintain laminar flow at much higher Reynolds numbers than found for rigid surfaces.
In the late 1950s, Max Kramer,* a German aeronautical engineer working in the United States, carried out a careful study of the dolphin epidermis and designed
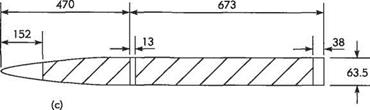
compliant coatings closely based on what he considered to be its key properties. Figure 8.34 shows his compliant coatings and test model. Certainly, his coatings bore a considerable resemblance to dolphin skin, particularly with respect to dimensions (see also Fig. 8.35). They were manufactured from soft natural rubber and he mimicked the effects of the fatty, more hydrated tissue, by introducing a layer of highly viscous silicone oil into the voids created by the short stubs. He achieved drag reductions of up to 60% for his best compliant coating compared with the rigid-walled control in sea-water at a maximum speed of 18 m/s. Three grades of rubber and various silicone oils with a range of viscosities were tested to obtain the largest drag reduction. The optimum viscosity was found to be about 200 times that of water.
Although no evidence existed beyond the drag reduction, Kramer believed that his compliant coatings acted as a form of laminar-flow control. His idea was that they reduced or suppressed the growth of the small-amplitude Tollmien-Schlichting waves, thereby postponing transition to a much higher Reynolds number or even eliminating it entirely. He believed that the fatty tissue in the upper dermal layer of
|
|
|
Fig. 8.34 Kramer’s compliant coating and model. All dimensions are in mm. (a) Cross-section; (b) Cut through stubs; (c) Model: shaded regions were coated Source; Based on Fig. 1 of P. W. Carpenter, C. Davies and A. D. Lucey (2000) ‘Hydrodynamics and compliant walls: Does the dolphin have a secret?’, Current Science, 79(6), 758-765 |
|
|
|
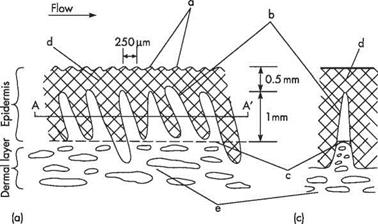
Fig. 8.35 Structure of dolphin skin, (a) Cross-section; (b) Cut through the dermal papillae at AA’; (c) Front view. Key: a, cutaneous ridges or microscales; b, dermal papillae; c, dermal ridge; d, upper epidermal layer; e, fatty tissue Source: Based on Fig. 1 of P. W. Carpenter etal. (see Fig. 8.34) |
the dolphin skin and, by analogy the silicone oil in his coatings, acted as damping to suppress the growth of the waves. This must have seemed eminently reasonable at the time. Surprisingly, however, the early theoretical work by Benjamin,[71] while showing that wall compliance can indeed suppress the growth of Tollmien-Schlichting waves, also showed that wall damping in itself promoted wave growth (i. e. the waves grew faster for a high level of damping than for a low level). This led to considerable scepticism about Kramer’s claims. But the early theories, including that of Benjamin, were rather general in nature and made no attempt to model Kramer’s coatings theoretically. A detailed theoretical assessment of the laminar-flow capabilities of his coatings was carried out much later by Carpenter and Garrad* who modelled the coatings as elastic plates supported on spring foundations with the effects of visco-elastic damping and the viscous damping fluid included. Their results broadly
confirm that the Kramer coatings were capable of substantially reducing the growth of Tollmien-Schlichting waves.
Experimental confirmation for the stabilizing effects of wall compliance on Tollmien – Schlichting waves was provided by Gaster[72] who found close agreement between the measured growth and the predictions of the theory. Subsequently many authors have used versions of this theory to show how suitably designed compliant walls can achieve a fivefold or greater increase in the transitional Reynolds number, Rexl, as compared with the corresponding rigid surfaces. Although, compliant walls have yet to be used for laminar-flow control, there is little doubt that they have the potential for this in certain marine applications. In principle, they could also be used in aeronautical applications. But, in practice, owing to the need to match the inertias of the air and the wall, the wall structure would have to be unpractically light and flimsy.*