Design of lifting bodies from known flowfields
8.2 Although we want to deal in the end with a fully-integrated propulsive lifting body, we may conveniently separate some of the problems and begin with the design of bodies which provide volume and lift together.
To get some idea of the possible performance and properties of waveriders, we consider first the simplest of them all, the Nonweiler or caret wing, at its design condition. How its shape is derived from the known exact solution for the inviscid flowfield of a twodimensional wedge has already been described in section 3.4 (see Fig. 3.9). We now want to find out roughly what the drag forces are that attend the provision of volume and lift for a family of bodies of this shape and of various lengths and spans and, in particular, we want to see whether the shapes which are efficient at high speeds have sufficient span for flight at low speeds. We must bear in mind, however, that these simple bodies cannot be expected to represent "practical" or "optimum" shapes in any sense.
For a family of such wings, each at its design condition with a plane shockwave contained between its leading edges, we include in the estimates the lift and pressure drag contributed by its compression surface and the skin-friction drag contributed by both its lower surface and its streamwise upper surface; but we do not then have any lift contribution from the upper surface and we ignore any drag contribution from the base.
A convenient set of geometric parameters to describe this family of shapes is (see Fig. 3.9):
6 , the initial wedge angle, which may also be interpreted as the angle of incidence of the body; s/й, the semispan-to-length ratio; from which can be derived
volume 1 . „ 1 „ч
t – —уте – = – у tan S, (8.2)
SJ// J і/і7й
which is a volume coefficient based on the projected plan area S = si. The wetted surface area excluding the base is then
|
|
the first term being the contribution from the upper surface and the second from the lower. Here the shock angle, о, enters the analysis; it is related to the mainstream Mach number, Mg, and the initial wedge angle, S, by
, 2 + (y – 1)M? sin2o
6 = a – tan ———- £— ——- * (8.4)
(y + 1)MQ sin a cos a
if we restrict ourselves to ideal gases. The analysis can thus be carried out in terms of the basic parameters s/й, t, and Mg ; all the others can be derived from these.
Waverider Aircraft
The uniform pressure over the lower surface is given by
![]()
![]() P ~ PC
P ~ PC
Vo
hence the lift coefficient
C – C cos 6 = —– Ц—- r
P (1 + 9t s/A)*
and the wavedrag coefficient due to both volume and lift
which is independent of Mach number, whereas, with skin-friction drag,
С,.- = C, S /S, included,
DF f w
where Cf is the usual skin-friction coefficient. In the subsequent examples, Cf is generally taken to be constant, Cf = 0.001 , to see more clearly what the general trends are.
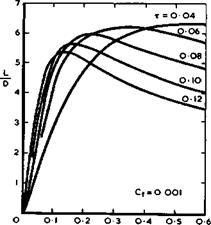
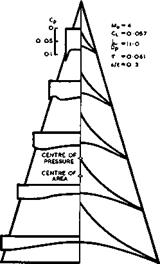
Some results plotted in Fig. 8.2 show that the lift-to-drag ratio has a maximum value at some value of the semispan-to-length ratio. This comes about because the effects of pressure drag and of friction drag have opposite trends: at higher values of s/A, the provision of a given volume coefficient requires larger initial wedge angles and hence stronger shocks; at lower values of s/A, the relative contribution from skin friction increases as a consequence of the larger ratio of wetted area to plan area. There is another feature of these results: at high values of s/A and also, of course, in inviscid flow, the thinner bodies give the better lift-to-drag ratios; but at sufficiently low values of s/A, the order is reversed and thicker bodies have a higher value of L/D than thinner ones. This is the opposite to what is generally true for linear systems with small perturbations where the drag contributions, especially those resulting from the volume and the lift, are essentially additive, to a first order. The unusual behaviour in the present case is partly due to the fact that the skin friction contribution increases as s/A decreases; it is also a consequence of the fundamental feature that volume and lift cere provided simultaneously by the same shockwave.
It is as well here to repeat, however, the caution sounded earlier, that these designs are not practical or optimum. In particular, the caret wing which has
LIVE GRAPH
Click here to view
|
Fig. 8.2 Lift-to-drag ratios of caret wings at Mq = 10 . After Collingbourne and Peckham (1966) |
small s/l, or low design Mach number, will be penalised by large anhedral and attendant skin friction drag. To remove this disadvantage, and thereby extend the envelope of profitable operating conditions, is the object of the generalisations mentioned later. For the time being, however, the analysis of caret wings will serve to direct our attention to the more promising combinations of parameters.
The characteristics outlined above indicate that the provision of volume is not such an exacting task at hypersonic speeds as it is with swept and slender wings at subsonic and supersonic speeds. There is an envelope to the curves drawn in Fig. 8.2, and even quite high values of т reach it at reasonably high values of L/D. This means that it should be possible to accommodate the large volume required for liquid hydrogen and to design efficient lifting bodies with t = 0.08 as a typical value (rather than т = 0.04 , which is typical for slender wings for supersonic flight).
We also find that good cruising efficiencies and hence the long flight ranges implied in Fig. 8.1 are reached at values of s/Jt, which lie in the range required to achieve good low-speed characteristics. Thus the indications are that the volume requirements and the low-speed and high-speed characteristics
are essentially compatible.
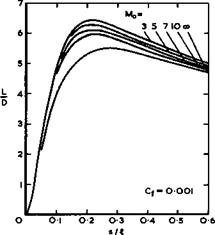
This compatibility is confirmed by the results in Fig. 8.3 for another family of caret wings with constant volume coefficient, designed for different Mach numbers between 3 and 10, with Mq = » shown as a limiting case (still for an ideal gas!). Because skin friction is included, L/D depends on the Mach number, unlike equation (8,8) for inviscid flow, but what is remarkable is the very small variation with Mach number. It would appear that, with this particular type of flow, the relative entropy increases associated with the provision of volume and lift do not increase rapidly with flight Mach number.
The actual maximum value of L/D depends, of course, strongly on the value of the skin-friction coefficient Cf. To see this a little more clearly,
LIVE GRAPH
Click here to view
|
|
|
Fig. 8.4 Lift-to-drag ratios of caret wings with т = 0.08 at
|
|
|
|
|
|
|
|
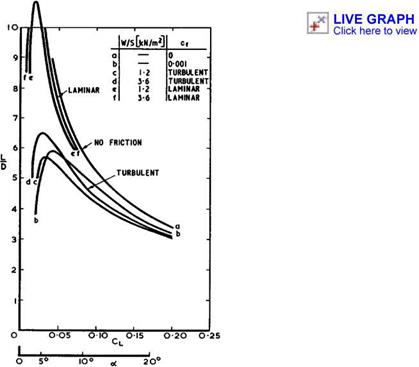
is kept constant and where the skin-friction coefficient has been estimated for laminar flow and for turbulent flow (as for boundary layers along flat plates with a length of about 30m) according to the actual velocity outside the boundary layer and the flight altitude implied. It should be noted that for an aircraft flying at high supersonic Mach numbers, the aerodynamic loading (L/S) falls below the wing loading (W/S) on account of the centrifugal effect: at M = 10 the difference amounts to about 15%. We find that the aerodynamic loading has not a large influence but that the state of the boundary layer has, especially in cases where the angles of incidence are low and the shockwaves weak. The curve for Cf = 0.001 may be regarded as representing roughly the case of turbulent boundary layers. These results indicate the importance of the effects of viscosity, which will be discussed in more detail in section 8.4.
Caret wings with plane shockwaves were originally proposed by T R F Nonweiler
(1959) and corresponding non-lifting bodies with star-shaped cross-sections by G I Maikapar (1959). Their properties have been calculated by D H Peckham
(1962) and by J R Collingbourne & D H Peckham (1966) who considered also the effects of an inclination of the upper surface to generate some (small) lift there, and of wing loading, flight altitude transition Reynolds number, and parasite drag. The lift and drag produced by a wedge in supersonic flow, either directly or by interference, has been calculated by P L Roe (1967).
There are many experimental investigations of caret wings, and we mention here those by L C Squire (1962), L Pennelegion & R F Cash (1962), D M Sykes
(1962) , D H Peckham (1964), L F Crabtree & D A Treadgold (1966), J Picken &
G H Greenwood (1965), К Kipke (1968) and (1970), G Hefer (1971), and U Ganzer
(1973) . The results always confirmed that the flowfield at the design condition is indeed as predicted, i. e. the shockwave is practically plane and attached to, and contained between, the leading edges, and the pressure is uniform over the compression surface. The effects of viscosity can be appreciable in model tests at low Reynolds number (e. g. К Kipke (1968) and G Hefer (1971)), but otherwise the flow model is not only simple but also realistic.
Nonweiler’s concept can be applied much more widely to construct more complicated shapes. For example, a delta wing with the cross section of the lower surface shaped like an inverted W, rather than an inverted V, will produce two plane shockwaves. L C Squire (1962) has pointed out that any shape formed by the intersection of a plane containing the shockwave with a cylinder of arbitrary cross-sectional shape supports a twodimensional flow.
If any element of the cross section has curvature, the leading edge will have a corresponding curvature in plan view. The concept may be extended to bodies supporting twodimensional flows with multiple shocks, leading to isen – tropic compression in the limit of the Townend surface already described in section 3.4, Figs. 3.10 and 3.11 (see L H Townend (1963) and (1967) and also J Pike (1972) where the concept has been applied to the design of supersonic sails). A C Southgate & J R Pedersen (1963) have pointed out that this concept leaves a wide choice to the designer of hypersonic vehicles, and-that this may prove valuable in satisfying trim and stability requirements over a wide speed range.
Waverider Aircraft
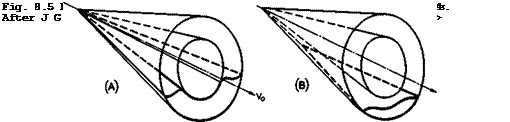 |
The possibilities are by no means exhausted with the flows discussed so far. In principle, much more general shock shapes may be prescribed and the shapes of the bodies, which support them, determined. This has been done, for example, by L W Schwartz (1974) for hypersonic flows generated by parabolic and paraboloidal shockwaves, leading to blunt bodies. We are more interested here in bodies with sharp edges and near-delta planform, and the method of J G Jones (1963) for designing lifting configurations from the flowfields of non-lifting cones is better suited for our purpose. This method was extended and generalised by В A Woods (1963), J G Jones & В A Woods (1968) and J G Jones et at. (1968). Conical flowfields are well known (see A Busemann (1929), G I Taylor & J W Maccoll (1933)) and well documented (see Z Kopal (1947) and D J Jones & W J Rainbird (1971)). Two simple cases of how this concept may be applied are illustrated in Fig. 8.5. A single shockwave is again used, but it is curved and forms part of the conical shockwave in the
flow past a right-circular cone at zero angle of incidence. The pressure over the compression surface is then no longer uniform, although the flow is conical about the apex of the original cone. Two types of compression surface may be distinguished. A surface of type A is formed by the streamlines which emanate from chosen leading edges along the shock cone, and which pass through the apex of the solid cone itself. These surfaces always contain part of the original cone surface and thus provide a concentration of volume near the centreline. The simplest shape of this type is the half-cone underneath a thin flat delta wing, with a shock attached to the leading edges, as proposed by A J Gggers (1960). A surface of type В is formed by streamlines passing through leading edges which do not come from the apex of the original solid cone but from a new apex which lies somewhere along the bottom generator of the conical shockwave. These shapes start initially like the flat-sided caret wings and then become more and more curved further downstream. There is thus a large variety of shapes readily available.
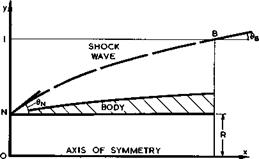
The Nonweiler concept has been extended to derive shapes of still greater generality by J Pike (1970). (See also P L Roe et al. (1971)). Pike studied in particular flowfields about annular bodies of revolution like that sketched in Fig. 8.6. The shape of the shockwave is again prescribed in advance and given by the equation
![]() (8.11)
(8.11)
The delta wings derived from this, with the apex at the point N, constitute
|
Fig. 8.6 Shockwave parameters 6ц, an<i R for body of revolution |
a five-parameter family, four of the parameters being contained in the shockwave equation and the fifth being the semispan-to-length ratio s/& . The angle 0{j controls the wing thickness and the pressure level near the nose of the configuration, and the angle 0g performs a similar function for the regions near the tips. The parameter R controls the type of flowfield, which corresponds to the flow about a pointed body of revolution when R = 0 and to a twodimensional flow when R = 1 . In all calculations carried out so far, the flow deflection in the base plane has been prescribed to be constant, with a value compatible with the shock strength at В. Fig. 8.7 shows on the right-hand side cross-sectional shapes and on the left-hand side pressure distributions for a typical configuration of this kind <0ц = 30°,
0g = 18°, n = 4, R = 0.1, s/i = 0.3, Mg = 4). It represents a considerable improvement over the earlier and simpler designs: it offers the choice of making the crosswise and lengthwise volume distribution more realistic and it gives a better aerodynamic efficiency at the same time (L/D =11, ignoring friction and base drag, whereas a corresponding caret wing would have L/D = 10 , by equation (8.8)). Pike also studied the effects of varying the
|
|
Fig. 8.7 Pressure distributions and sections of a configuration derived from the flowfield of Fig. 8.6. After J Pike five parameters for Mq = 4 . The angle 0g cannot be reduced much below 18° without making the wing thickness too small at the tips, or increased much above 18° without causing the value of L/D to fall. The other parameters have only a very small effect on the lift coefficient. From the view point of aerodynamic efficiency, the best value of s/i is slightly below 0.3; values slightly above 0.3 give a more realistic wing geometry. Increasing the parameter R from 0 to 1 has the effect of steadily increasing the anhedral angle and producing a rather flat maximum in L/D at about R = 0.2. An increase in the angle 6ц reduces L/D by only a small amount but increases the anhedral angle markedly. The curvature parameter n has almost no effect on L/D, but it can be used to reduce the amount of anhedral. A simultaneous increase of both вjj and n can improve the overall geometry by concentrating the volume further forward, without sacrificing the aerodynamic efficiency appreciably.
A problem that has received much attention is that of finding ‘optimum shapes ‘ for lifting bodies of given lift and volume. We should note from the outset that this approach is rather restrictive: if we are interested in the design
of complete aircraft, we should consider propulsive lifting bodies, and we shall see in section 8.6 that when this is done the resulting shapes may be derived from lifting bodies but are not necessarily based on the more restrictive optimum shapes. Generally, we cannot expect that any ‘optimised’ calculated shape could do anything more than provide a guide to the designer. Therefore, we give only a very brief account of attempts at deriving optimum lifting bodies, following the summary given by P L Roe (1972) (see also A Miele (1965; J D Cole & J Aroesty (1965); J Pike (1966); P L Roe (1969);
A L Gonor (1973)).
We should be aware also of the enormity of the work involved in a really general and soundly-based solution to the problem of optimisation of shapes. First of all, we should need a computer program capable of calculating the inviscid flow past a general threedimensional wing-like shape. For this program to inspire real confidence, it would have to be based on the complete Euler equations of inviscid motion, and its logical structure would have to be sophisticated enough to take account of shockwaves in locations which are not known a priori, possibly embedded in the flow field as well as attached to the leading edges. Simplifications are needed and would follow if we could assume that the shockwave was attached everywhere, so that the upper and lower surfaces were independent. The solution is also greatly aided if the assumption of conical self-similarity can be made and if the flow near the leading edge is like that past a yawed wedge. But, in principle, it would be necessary to specify the unknown shape by a large number of parameters, and to treat all these as independent unknowns in some sort of multidimensional search technique, the strategy of which would form a research subject in itself. The solution for inviscid flow would then have to be combined with a really good analysis of threedimensional compressible boundary layers. It is clear that we cannot hope for a general solution for quite some time to come. Therefore, the purpose of this kind of theory should be to provide a catalogue of ‘good’ shapes, together with the assumptions used to obtain them, and some sort of explanation of the way these assumptions are reflected in the geometry of the shapes.
As an illustration of existing optimisation methods, consider the very simple case of a twodimensional body z(x) of unit chord and cross-sectional area
1
A = J (1 – x) dx (8.12)
0
on the assumptions that the upper surface lies along the mainstream and that the base drag can be ignored. We also use approximate solutions of the equations of motion and assume that the pressure over the lower compression surface has the form
This includes as special cases (I) linear theory, when
![]() C, – 2/8 , C2
C, – 2/8 , C2
(2) Busemann’s second-order theory, when
(3)
Newtonian theory for slender bodies, when
To obtain the minimum value of CD for given values of CL and A leads to a differential equation for the contour of the lower surface:
2Cli+3C2(i)2 + Xl(Cl + 2C2f) + X2(1-x> = 0 * <8*,6>
![]()
![]()
where Л] and Л2 are Lagrange multipliers. In the special case of linear theory, this reduces to
which can be integrated:
z(x) = – XjX + ~~ £(1 – x)2 – lj
 That is, the optimum contour is parabolic, with Xj and the required values of and A. We note that
That is, the optimum contour is parabolic, with Xj and the required values of and A. We note that
1
z(D “ /І dx = CL/C1 *
0
i. e. all wings having a given lift pass through the same point in the base plane. Of these, the one with the least drag of all is the wedge which leads to the caret wing in a threedimensional flow. If we actually need a greater cross-sectional area than that of the wedge, for the same lift, the best way of adding the extra area is by means of a ■parabolic curve. If, on the other hand, we need less area, the best policy would be to use the wedge section since this has less drag than any other and offers without penalty a bonus volume over and above our needs. What matters too, is the question of whether the volume distribution is such that the centre of gravity is in the right place so that the aircraft can be balanced and brimmed.
The same general conclusions hold in the non-linear case C2 Ф 0 . The detailed shape of the section is altered but can still be expressed analytically in the form of a power law in x. The compression surface is still convex, and the effect of adding the non-linear term is to concentrate the volume further aft. Results showing the same general trends have been obtained by G J Maikapar (1966) and R S Bartlett (1966). It may seem somewhat surprising that it pays to generate a given overall lift by having a stronger shockwave, and more lift, over the front part than the corresponding wedge and then having some expansion, and taking lift off, over the rear. One might have expected that, on the contrary, a concave surface with a centred compression of a large number of weak waves (as in Fig. 3.10, leading to the
Townend intake surface in Fig. 3.11) should be more efficient than the wedge flow with one shock (as in Fig. 3.8, leading to the caret wing in Fig. 3.9).
That this is not so may be explained by a more detailed consideration of the
final downward deflection of the captured mass of air, which is needed to generate a given lift force; the smaller the mass of air captured and the larger the downwash imparted to it, the higher will be the drag force for a given lift.
To obtain reliable answers requires a good theory, and there are some doubts as to whether any of the approximations used above are sufficiently accurate. But to treat even the twodimensional flow with any greater accuracy than this would be a formidable task. Again, we should bear in mind that the general conclusions may be quite different when propulsion is included and consideration given to energy addition to a captured airstream, which will affect lift and thrust and drag as well as volume and trim.
All the bodies discussed so far were assumed to have a streamwise upper surface and hence a certain base area. Such a base is not likely to be acceptable in a real aircraft design, so that means must be found to eliminate it. Again, the inclusion of propulsion provides a natural means for this purpose (see section 8.6). Here, we describe some ways of how this purpose may be achieved by shaping the upper surface.
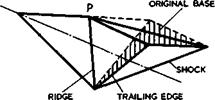
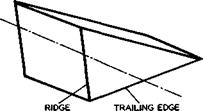
A very simple way of modifying a caret wing to have no base area but a sharp tra-Lling edge is illustrated in Fig. 8.8(a). The lower edge of the original base is the new trailing edge, so that the flow over the compression surface remains unaltered. The front part of the upper surface is still streamwise, but then two swept ridge lines from a point P to the wing tips are incorporated and two sloping plane surfaces from these ridge lines to the new trailing edge. Such an afterbody shape was first proposed by A A Griffith
(1956) , with a view to achieving a low afterbody drag. In principle, there could be a Prandtl-Meyer expansion around the ridge lines, which directs the flow inwards towards the plane of symmetry. To turn it back into the mainstream direction could involve a useful, and possibly drag-reducing, recompression process. This recompression could be continuous, and L R Fowell (1955) has given a criterion for the maximum deflection angle below which the compression should be shockless. The criterion itself has been questioned by В M Bulakh (1958), but there is agreement that there should be a shockwave if the deflection angle is an ‘over expansion’ exceeds some value. What happens in a real flow has been investigated by D A Treadgold (1960) on a simplified model illustrated in Fig. 8.8(b). There are again two ridge lines behind a
|
(a) MODIFIED CARET WING |
|
|
(b) BODY TESTED BY PIERCE « TREADGOLD
Fig. 8.8 Afterbody shapes downstream of ridge lines.
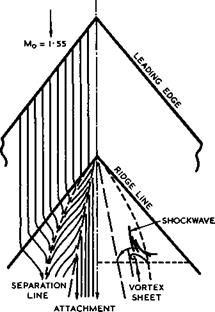
streamwise forebody of constant chord, to give the same Mach number and boundary-layer conditions along the ridges. The ridge lines are nominally near-sonic, i. e. the Mach number component normal to the ridge is near unity. The afterbody is a single plane surface sloping down at an angle of 23° relative to the forebody. Typical experimental flow patterns are given in Fig. 8.9, where the left-hand side shows limiting streamlines in the surface and the right-hand side an interpretation of the flow, based in part on
Waverider Aircraft
|
LINE Fig. 8.9 Flow pattern over body of Fig. 8.8(b). After Treadgold |
observations using a conical shadowgraph technique developed by D Pierce &
D A Treadgold (1964) (see also V N Alekseev & A L Gonor (1974)). We find that there is indeed a Prandtl-Meyer expansion around the ridges; when the ridges are nominally supersonic, the measured pressures agree remarkably closely with calculated values (note that linearised theory would wrongly predict a suction that tends to infinity as //a, where n is the distance normal to a sonic ridge line). This close agreement is the more remarkable since there is a clearly-visible upstream influence in the boundary layer such that the streamlines in the surface begin to turn well before the ridge line is reached. Downstream of the ridge line, the viscous flow, subjected to a strong adverse pressure gradient, turns into a separation line well before it reaches the centre line. The flow is not conical about the apex of the afterbody. Since the separation line is highly swept, the resulting separation surface is a vortex sheet, as described in section 2.4, Fig. 2.12. Inboard of the separation line, the viscous flow drawn into the core of the vortex sheet is actually directed outwards, away from the attachment line which is associated with the vortex sheet. The attachment surface divides the air which is drawn into the vortex core from that which is not and forms a nearly-parallel stream near the centre line. The inviscid external stream follows a quite different pattern: it is always directed inwards, and the turning is achieved mainly through a shockwave which is situated above the vortex sheet. Thus we have a fundamental flow pattern, where changes in the direction of the flow are required, and where these are achieved in different ways in the viscous region and in the inviscid region. With afterbodies of this kind, the drag is not likely to be low and the designer of an aircraft cannot be expected to use them, but we shall meet similar types of flow again when we discuss off-design conditions in section 8.3.
We can infer from this that we must look for other and less simple types of flow if we want to shape the upper surface of waverider aircraft, possibly with the aim of making the upper surface also contribute to the lift. The streamline-tracing technique from known flowfields can again be used so as to preserve the calculable nature of the flow. The simple expansion surface of J W Flower (1963), based on the twodimensional Prandtl-Meyer expansion has already been described in section 3.4, Fig. 3.12. The construction of Flower’s expansion surface necessarily implies that the keel is directed downwards from the mainstream direction and that the leading edges must lie in a Mach plane whose inclination is о = sin”l(l/Mg) , i. e. they are directed upwards if they are swept back. These features introduce a matching problem if such an expansion surface is to be joined onto a compression surface. For example, the leading edges of the expansion surface, which have dihedral, cannot be joined to the leading edges of a caret compression surface, which have anhedral. Flower has pointed out that his expansion surface can be joined more readily onto two or three caret surfaces so that the complete configurations have cross sections in the form of a Y or an X. But this may introduce large surface areas and hence friction losses. It is, therefore, worthwhile to generalise the approach, and to turn away from twodimensional to axisymmetric flowfields as a basis.
Suitable streamsurfaces, which are relatively flat, may be found in the flow – field over the tapering rear end of a body of revolution, as described by К C Moore (1965) and J G Jones et at. (1968). The most promising technique employs an ingenious idea by J Pike (1966): two axisymmetric expansion flows are placed side by side in such a way that their Mach cones intersect. A streamsurface can be drawn which starts upstream of the expansion regions and is initially parallel to the mainflow. As soon as it enters either expansion region it curves inwards. Any interaction between the two fields can be prevented by placing a vertical fin surface between them. The overall geometry can be chosen in such a way that the two sides of the fin surface also conform to streamsurfaces of the two flows. The particular advantage of this method lies in the fact that volume may be selectively removed from midsemispan positions and remain concentrated near the middle. The resulting volume distribution may help to solve the ‘packaging problem’ which is typical of hypersonic aircraft, where items requiring relatively large volumes must be stowed away.
To see the design of lifting expansion surfaces in perspective, we must remember two aspects. One is that the lift generated by suction can never be a large portion of the overall lift and will decrease with increasing Mach number, simply because vacuum conditions may be reached and set a limit to it, as has been discussed already in section 6.4 in connection with Fig. 6.38.
The other is the difficulty that the expanded flow must be compressed again somehow somewhere near the trailing edge which is likely to be unswept. For example, the streamlines over Flower’s surface are straight in planview and no recompression takes place over the surface. A shockwave at the trailing edge might then bring the pressure and the flow direction back to mainstream conditions, but this will introduce the familiar shockwave/boundary-layer interaction problem. It is possible that the upstream influence of the shockwave in the boundary layer may reach quite a long way upstream and that strong shocks may cause a bubble separation, which induces positive pressures over the surface that counteract or even reverse part of the suction produced by the expansion. Not much is known about this effect and about what would be a reasonable course to take in aircraft design. It is clear, however, that the emphasis in the aerodynamic design of hypersonic aircraft should be on the design of the compression surface.