Displacement of Points

Let us recap: The location of a point is meaningless unless it is referred to a reference point. So, for instance, the location of the center of mass (c. m.) of a missile В must be related to a tracking station, the launch point, or the target coor­dinates. The term displacement implies that mutual relationship. If the reference point is R, then the displacement vector of the missile is sbr. Its time dependency is expressed by sbrU). The displacement of a point is an invariant tensor concept, valid in any allowable coordinate system. For computational attainment this first – order tensor must be expressed in a coordinate system to be processed numerically. For instance, the missile may be measured in the tracking station coordinates ]я. Then the displacement vector’s coordinates are

‘іі(Г)"

S2(t)

Example 2.4 Helical Displacement

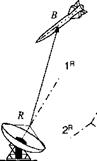
Problem. A missile makes an evasive circular maneuver toward a tracking radar R. Its closing speed is v, revolving at the angular velocity со on a helix of radius r. Suppose the Iя direction of the radar coordinate axes is parallel to the helix centerline. Formulate the displacement vector of the missile wrt to the radar in radar coordinates.

Solution. You should be able to verify the result with the help of Fig. 2.11.

—vt

r cos(wt) r sin(<uf)

For emphasis I point out that the coordinate axes are completely defined by di­rection and sense. They are free floating without origin. Drawing them from a common point, as I have done in Fig. 2.11, is convenient but unnecessary.