Dyadic Product

The third possibility is the multiplication of vector x with the transpose of vector у to obtain tensor Z,

xy = Z

which represents, for any allowable coordinate sy stem ]A, the matrix multiplication

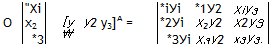
мАшА = [z]A

We borrowed the name dyadic product from vector mechanics, which avoids ten­sors by decomposing them into vector form and calling that hybrid construct a dyad. We have no need of dyads themselves, having committed ourselves to mod­eling flight mechanics by tensors only.

If both vectors x and у are one and the same unit vector u, then the dyadic product produces the projection tensor P. Given any vector t, its projection on the и direction is the vector r, resulting from

r = Pt with P —ий (2.21)

You can easily convince yourself of that fact by substituting the definition of P into Eq. (2.21) r = uUt and recognizing that the scalar product Ш gives the length

and и the direction of vector r. In any coordinate system, say ]A, the projection tensor has the form

u	UU2	U j М3
M2M1	uj	M2M3
M3M1	ИЗИ2	u

[P]A = [и]А[й]А =

It is a symmetric matrix because the scalar product of coordinates is commutative.

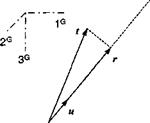
Example 2.3 Thrust Vector Projection

Problem. The direction of the centerline of a missile is given by the unit vector

[m]g = [0.2 0.3 —0.9327] in geographic coordinates. To make a course correc­tion, the gimbaled rocket motor turns the thrust vector away from the centerline to a position given by [f]G = [7.6 12.8 —36] kN. Determine the thrust vector along the centerline of the missile [r]G in geographic coordinates. (See Fig. 2.10.)

Solution. We just substitute the values of the example into Eq. (2.21) and calculate the centerline thrust vector

[r]G = McmG[t]G =	– 0.2 – 0.3	[0.2 0.3 -0.9327]	-7.6′ 12.8	_	‘ 7.787 – 11.681
	-0.9327		-36		-36.317

The matrix product can be executed any two ways. Either first calculate the pro­jection tensor and multiply it with the thrust vector, or evaluate the scalar product first and then multiply it with the unit vector. Both options lead to the same result.

We have come to the vista overlooking the foundations of mathematical model­ing of aerospace vehicles. Classical mechanics is the environment, and Cartesian tensors are the building blocks. We reviewed the axioms of mechanics as well as the Principle of Material Indifference and postulated the sufficiency of points and frames as modeling elements. Simple Cartesian tensors are our language with em­phasis on the invariant, coordinate-free formulation of physical phenomena. There are many more overlooks still ahead. However, we pause and apply our newfound skills to some important geometrical modeling tasks.