Elliptical orbits

So much for circular orbits – now what about the elliptical orbits which, as we have already explained, are much more common for artificial satellites? They are also more common in nature, the orbit of the moon round the earth being one of the few examples of a nearly circular orbit.

Mathematically it is a little more difficult to calculate what happens during an elliptical orbit when both the velocity and the radius are constantly changing, but the reader who has followed the arguments so far should have no difficulty in understanding the principles involved. Returning to horizontal launches from a height of 800 km it will be remembered that at a speed of launch of 7.48 km/s the orbit was circular, below and above this speed it was elliptical, though at the escape velocity of 10.7 km/s it became an open curve, a parabola, and then above this a hyperbola. The real criterion is how much energy, kinetic energy, the body has when it is launched; because it is this energy which enables it to do work against the force of gravity – it is really much more like the case of the stone that was thrown vertically upwards than might at first appear. In vertical ascent the kinetic energy given to the body at the launch enables it to do work against gravity and so gradually acquire potential energy; at the highest point reached all the kinetic energy has become potential energy; then as the body falls again the potential energy is lost and kinetic energy regained until on striking the ground the original kinetic energy has all been regained (neglecting air resistance of course). The body travelling on a curved path also has to work against gravity, is also accelerating all the time, and downwards, just like the body on the vertical path, and in fact, at the same rate – once that is understood, all is clear.

The only difference then is that on curved paths the body must retain some of its kinetic energy throughout the circuit if it is to continue on its orbit. At a launching height of 800 km it has at the start both kinetic and potential energy; if the launching speed is less than the circular velocity of 7.48 km/s, but sufficient to ensure that it doesn’t come down to earth before reaching the far side, then by the time the body reaches the far side of the earth it will have dropped in height, i. e. lost some of its potential energy, but by the same token will have gained some kinetic energy (just like the falling stone), and so will be travelling faster – at over 7.9 km/s in fact if it is near the earth’s surface. Then as it returns to the starting point it will gain potential energy, rising again to 800 km, and lose kinetic energy, until the proportions (and values) are the same as they were at the launch. In all this we are still neglecting air resistance, and it is air resistance which in practice makes an orbit of this kind imposs­ible; for as soon as the body travelling round the earth, and getting lower all the time, meets appreciable air density, it will experience drag, and in working against this will lose kinetic energy and so the speed necessary to take it round the far side of the earth. Thus it will fall to the ground before getting half way round or the heat generated by kinetic heating will cause it to burn up.

As the launching speed gets nearer the circular velocity, the body will keep clear of appreciable atmosphere all the way round, and the orbit becomes more practical. But until the circular velocity is reached the launching point will be the apogee, and the perigee will be on the far side of the earth, where the body will be nearer the earth’s surface, and where the velocity will increase until, at the circular velocity, it remains constant all the way round.

As the launching speed is increased above the circular velocity, the body will have more kinetic energy than is necessary to keep the 800 km of height, and so it will gain height and potential energy, at the same time losing speed and kinetic energy, until it passes round the far side of the earth – now the apogee – at lower velocity and greater height. And so it will go on as the launching speed is still further increased, the ellipse becoming more and more elongated, the apogee getting farther and farther from the earth, and the residual velocity at the apogee getting less and less.

As the launching velocity approaches the escape velocity of 10.7 km/s, the body at the apogee will only just have sufficient kinetic energy to enable it to get over the top, as it were, and return again to earth. If launched at the escape velocity, or above, it won’t even be able to do this, and it will go off into space on its parabola, or hyperbola as the case may be, at the mercy of the gravita­tional attraction of some other body, probably the sun. This new force of attraction will restore its kinetic energy and velocity as it embarks on a com­pletely new orbit, possibly of enormous size like that of the earth round the sun (radius of orbit about 150 million kilometres).

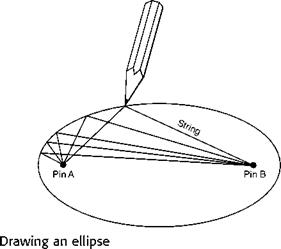
Since nearly all practical orbits are in the form of ellipses it is interesting to consider some of the properties of these curves. The reader may know that an ellipse can be drawn on paper with a pencil and a piece of string of fixed length attached to two pins (Fig. 13.7, overleaf). In other words, an ellipse is the locus of a point moving so that the sum of the distances from these two points (the pins) is constant. These points are called the foci of the ellipse – in a circle, which is only a particular case of an ellipse, they coincide – and it will be noticed that in the figures illustrating the paths of satellites the centre of the earth is always one of the foci of the ellipse.

At launching speeds below the circular velocity the centre of the earth is the focus farthest from the launch, at the circular velocity it is of course the centre of the circular orbit, and at higher launching speeds it is the focus nearest to the launch, the other focus getting farther and farther away as the launching speed is increased. For launches at the escape velocity the distant focus has gone to infinity, and only one focus is left at the centre of the earth – a para­bolic curve has only one focus. Above the escape velocity, too, the hyperbolic

curve has only one focus (see Fig. 13.8); strictly speaking, a hyperbola has two foci, but this is because there are two parts of the curve, back to back as it were, and we are here only concerned with one part of the curve.

It is not of practical importance in understanding the mechanics of projec­tiles and satellites, but it may be of interest to know that these curves are all derived from a cone (they are the intersections of a plane and the surface of a cone) and are sometimes called ‘conic sections’ (Fig. 13.9).