Estimating the induced velocity

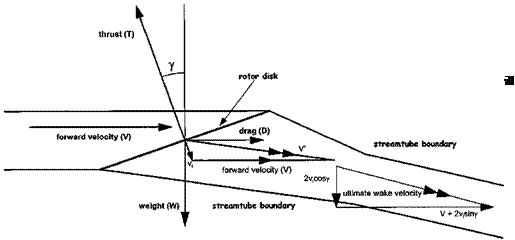
If a helicopter in horizontal flight at speed V (see Fig. 2.10) is considered then in order to sustain level flight the rotor disk must be tilted forward. This is so that the thrust vector, T, can provide both the forward propulsive force (Tsin y) and support the weight of the helicopter (Tcos y). Now the rotor will induce a flow through itself at right angles to its plane of rotation. The combination of the forward speed, V, and this induced velocity, v1, is the oblique flow across the disk, V’. From Equation (2.10):

T

v =———

1 2pAV’

and from Fig. 2.10:

V’ = V(V + V1 sin y)? + (v1 cos у)? = V(V? + 2Vv1 sin yv?

Also:

Thus:

or:

___________ 1__________

cos у V V? + 2 Vv1 sin у + v?

1

‘VV2 + v2

and using the quadratic solution of V4 with a positive root:

_ , V 2 V4

v=-l _t+vt +1

which can be approximated at higher forwards speeds, when V is much greater than V,, by:

W

v =—–

1 2pAV

Figure 2.11 shows the predicted variation of induced velocity ratio with forward velocity ratio. At speeds in excess of twice the induced velocity in the hover the simple approximation can be used. (For the example helicopter this equates to a forward speed of around 30 m/s or 60 KTAS).

1.7.1 Estimating the ideal power:

From Fig. 2.10 it can be seen that by using Equation (2.11) it is possible to write the ideal power in coefficient terms:

PDEAL T (V sin у + V,) DV + Tv, 13/ f

where f = SCD = drag area (area of flat plate that produces equivalent drag to helicopter body) and p = advance ratio (V/VT). Thus the ideal power coefficient comprises two components: one proportional to the cube of the advance ratio – the parasite power; and one proportional to the inflow ratio (X) – the induced power. Figure 2.12 shows the variation of ideal power coefficient for the example helicopter, note the presence of the familiar ‘power bucket’.