Going to the moon?

Now let us get just a little nearer to the true state of affairs by realising at least the existence of the moon. How will this affect the stone that is thrown verti­cally from the earth?

Fig 13.8 (a) a parabola, (b) a hyperbola

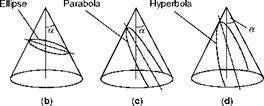Fig 13.9 Conic sections

In (a) the plane cuts the cone at right angles to the centre line, forming a circle. In (b) the plane is at an acute angle to the centre line, but the angle is greater than a, forming an ellipse. In (c) the angle is egual to a, forming a parabola. In (d) the angle is less than a, forming a hyperbola.

Well, it will affect it quite simply, in principle at any rate, in that there will now be three masses all attracting each other – the stone, the earth and the moon.

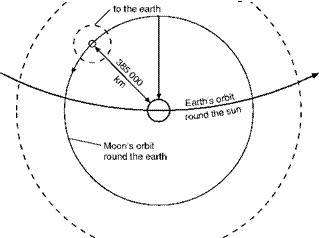
The moon is about 385 000 km away from the earth. Just for the moment let us suppose that it remains over the point on the earth’s surface from which we throw the stone, and that we increase the starting velocity of the stone until it reaches distances of 6370 km, 12 740 km, and so on. As before, the weight will decrease with the distance from the earth’s surface, but now rather more so because a new factor has been introduced, the attraction between the moon and the stone. The mass of the moon is only about 1/81 of the mass of the earth, so the force of attraction at the same distance will only be a fraction of that of the earth (1/81 in fact), but as we know the moon’s attraction is a very real thing, even at the earth’s surface, for it is largely responsible for the tides.

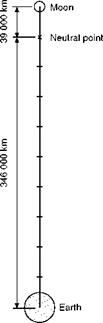
We have already imagined so much that we may as well go one step further and imagine that our stone travels in a straight line between earth and moon. As it gets nearer to the moon the attraction of the earth will decrease and that of the moon increase, until a point is reached where the two attractions are the same. Since the force is inversely proportional to the square of the distance, the distance from the centre of the moon at which this occurs will be 1/V81 of the distance from the centre of the earth, or approximately one ninth (Fig. 13.10, overleaf); roughly say 39 000 km from the moon and 346 000 km from the earth. So if a stone is launched with just sufficient velocity to reach this point, it will stay there – and will once more be ‘weightless’, this time perhaps more correctly so, though again we notice that it is just a question of the forces being balanced. In fact the balance is too delicate, and the stone will not in fact stay at this neutral position, because some other heavenly body will attract it and tip the balance, and it will fall either onto the earth or the moon. If the stone is launched with a velocity slightly greater than that required to reach this neutral point, it will still be travelling towards the moon at this point, and since as it passes the point the attraction of the moon will become greater than that of the earth the stone will pick up speed and fall on to the moon.

It has already been emphasised that all bodies attract all other bodies, and that therefore one can never really escape from the gravitational attraction of all the bodies in the heavens. But the motion of a body in space becomes extremely complicated if the forces of attraction on it of even three bodies (such as the sun, the moon, and the earth) are taken into account, and for this reason it is convenient – and not very far wrong – to consider a zone of influ­ence for each body, this being a sphere in space in which that particular body has a greater gravitational effect than a larger body. The earth, of course, is well within the sun’s zone of influence – its motion round the sun is in fact con­trolled by the force of attraction between it and the sun – but on the other hand, bodies near the earth’s surface, although attracted by the sun, come much more under the influence of the earth’s attraction than that of the sun (which is perhaps just as well, since otherwise we would all be off to the sun). The attraction of the earth remains greater than that of the sun for a distance of about a million kilometres, so the earth’s zone of influence relative to the sun is a sphere of about one million kilometres radius (Fig. 13.11). Similarly the moon’s zone of influence relative to the earth is a sphere of about 39 000 km radius – as we discovered in the last paragraph, though we didn’t give it that name.

Well, we have described one way of getting to the moon – to go straight there in fact – but it is not quite so easy as it sounds because of the great accu­racy needed both in aim and launching speed. As regards aim, we have made

Fig 13.10 Neutral point between earth and moon

things much too easy in our imagination; in reality the earth is travelling round the sun, and is spinning on its own axis, while the moon is travelling round the earth. But even more interesting is the sensitivity to exact velocity.

The distance of 385 000 km to the moon is much less than the distance to infinity, only a minute fraction of it, and to the neutral point even less, but it requires nearly as much energy to reach this distance as it does to reach infinity because the attraction of the earth at this distance has been so reduced that nearly all the serious work in overcoming the earth’s gravity has already been done; or, putting it another way, whereas 11.184 km/s is needed to send the stone to infinity, about 11.168 km/s is needed to send it to the neutral point from which it will drop on the moon. So if launched at less than 11.168 km/s it will return to earth; at about 11.168 km/s it will go to the moon; at 11.184 km/s it will go to infinity (it could hit the moon on the way); and at over 11.184 km/s – well, we have mentioned that before.

The mass of the moon being so much less than that of the earth, its escape vel­ocity is only about 2.4 km/s, and that is the speed at which the stone would arrive on the moon if it ‘fell’ from infinity; it will for all practical purposes be the same if it falls the 39 000 km from the neutral point. This is about the muzzle

Fig 13.11 Zones of influence Not to scale.

velocity of a shell as it leaves a long-range gun, and so the landing on the moon will not be a very soft one, and this is the minimum speed at which the stone can arrive unless there is some means of slowing it down; there is no ‘atmosphere’ to do this, and the only hope is to break the fall by rockets fired towards the moon.