Ground effect

Proximity to the ground results in a decrease in the induced power to produce a given thrust. The presence of the ground is effectively the same as that of having a mirror image rotor below ground. The slipstream of the image rotor induces an upward velocity at the real rotor so that the inflow velocity will be reduced and the incidence of the real rotor increased at constant pitch or feather angle. Hence, the lift developed by the real rotor is increased and the induced power required to maintain a hover is reduced.

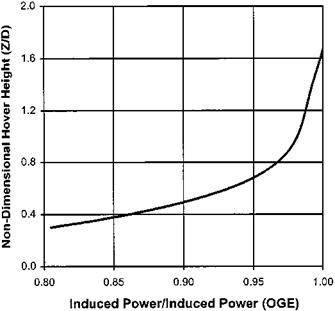
Figure 2.6 shows the general trend in the form of a graph of the ratio of the induced power required in and out of ground effect against the height of the rotor above ground (Z), non-dimensionalized by the rotor diameter, D. We can see that ground effect decreases with increasing height, effectively disappearing at about one rotor diameter from the ground. Empirical relationships exist which describe the variation of power, in-ground-effect, with hover height [2.4]. One example is:

2.2.3 Tip loss and non-uniform flow

A characteristic of the actuator disk theory is that the linear theory of lift is maintained right out to the edge of the disk. In reality, because the rotor consists of a finite

number of blades, some air is able to escape outwards, from the streamtube, by the action of the tip vortices. The total induced flow is thus less than the actuator disk theory would prescribe. This deficiency is called tip loss and is shown by a rapid reduction in lift over the last few per cent of the span near the tip. It is common practice to account for this discrepancy by assuming that beyond a certain outboard station the blade sections develop drag but no lift. Thus the thrust integral becomes:

1 fBR

CT = 2 sal (6r2 – ^r)dr

Jo

This increases the hover power to:

C = 1 C 3/2+ — C or C =^— C3/2 + – C

C = BV2 C 3 + 8 Cd° or Cp = V2 C 3 + 8 Cd°

In 1927, Prandtl and Betz approximated the tip loss factor, B, to:

Goldstein and Lock showed satisfactory correlation with this approximation for lightly loaded rotors [2.9]. The value of к can be increased slightly to account for the losses incurred due to the non-uniform nature of the swirling flow from a real rotor. Typical values for к vary between 1.13 [2.4] and 1.15 [2.10].