Improved predictions

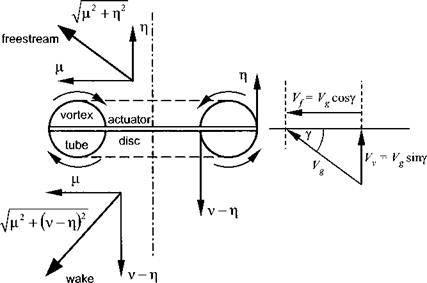
The ‘Wolkovitch’ boundaries although based on a detailed representation of the vortex-ring condition fail to match empirical data. Experience gained from wind tunnel experiments and flight test suggests that the vortex-ring condition can be escaped by allowing a forward velocity component to develop. Thus the lower boundary should show that as the horizontal velocity (q) is increased higher rates of descent (q) are required to enter the vortex-ring state. This can be achieved if the Wolkovitch approach is modified to account for the effect of forward speed on the wake geometry, see Fig. 2.20.

Fig. 2.20 Modified Wolkovitch analysis of the vortex-ring state (adapted from [2.27]).

Figure 2.20 shows that the magnitude and direction of both the freestream flow and the wake can be represented by vectors:
a = freestream flow = vV2 + Ц2 b = wake = V^2 + (v _ q)2
Now the dot product (b^a) can be thought of as the magnitude of one vector multiplied by the component of the other vector in the direction of the first. Thus in this context the dot product represents the magnitude of the wake velocity multiplied by the component of the freestream in the direction of the wake. Hence:
b-a TbT
component of freestream flow in direction of wake
b-a_ p x p + (v _ q) x_ q = + q(q _ v) Ib I Vp^+Cv^n)2 Vp2 + (v _ q)2
The Wolkovitch approach assumes that the vortex-ring state begins when the velocity of the vortex tube relative to the actuator disk is zero, that is:
t2 + q(q _v) VTJT(v_f
Therefore: p2 + q(q _ v) + p2 + (v _ n)2 = 0 2p2 + 2q2 + v2 _ 3qv = 0
or:
3 1 p2 = 2 qv _ q2 _ _ v2
(2.23)
As before from momentum theory, 1 = v2(p2 + q2 _ 2qv + v2), thus:
1 = v2 (3qv _ q2 _ 1 v2 + q2 _ 2qv + v2 ) = v2 (1 v2 _ 1 qv
2 = v4 _ qv3 2 q = v v3
And, returning to Equation (2.23):
A V 1 2 = 1 4 v v3 ) 2v v2 v6
3	2

Therefore the lower vortex-ring boundary is given by:

2

ц = v——

VJ

2 1 4

p = 7 – V6-

The upper vortex boundary is obtained in an analogous manner, by replacing v with kv in Equation (2.23). As mentioned above, Wolkovitch recommended k = 1.4 as denoting the edge of the fully developed vortex ring condition. Peters and Chen [2.22], on the other hand, prefer k= 2 as indicating the condition beyond which no vortex is present anywhere in the streamtube. Hence Equation (2.23) becomes:

31

p2 = 2 ^2v) — ц2 — ^(2v)2 = 3^ — ц2 — 2v2

Once again from momentum theory, 1 = v2(p2 _|_ ц2 — 2^ + v2), thus: 1 = v2(3^ — ц 2 + ц2 — 2v2 — 2цv + v2)

1 = v2^v — v2) = — v4

1

Ц = v + —

v3

Consequently:

Therefore the upper vortex-ring boundary is given by:

1

Ц = v + —

v3

These boundaries are shown in Fig. 2.21. Clearly the lower boundary approximates to the empirical trend whereby with forward speed higher rates of descent are required to enter the vortex-ring state. There are, however, two issues that remain unresolved. First the upper and lower boundaries should predict the same forward velocity, above which vortex-ring can be completely avoided. Secondly the upper boundary is based on entry to the windmill-brake state (Vv = 2vih in the hover) whereas the lower indicates entry into fully developed vortex-ring (V = 0.7vih in the hover). In order to resolve these problems the lower boundary must be further modified to start at p = 0, ц = 0. This is achieved by noting that a vortex will appear in the streamtube when (b-a)/ Ib|< 0. Thus the lower boundary should be given by:

p2 + ц(ц — v)

V^2 + (v — ц)2

Fig. 2.21 Vortex-ring boundaries using modified Wolkovitch analysis.

Applying momentum theory gives:

1 = v2(^v — Ц + Ц — 2qv + v2)

1 = v2(v2 — цу)

1

Ц = v ——

Consequently:

^2=3v (v—УЗ)—(v—УЗ)— 2у2=У2—У6

Therefore the complete criteria, see Fig. 2.21, for the vortex-ring state are:

1

Ц = v±—

2 1 1

^ = 7 — У6

These criteria can be used to predict a complete and coherent boundary for the onset of the vortex ring condition [2.22].