Maximum Flight Speed for a Jet Aircraft

In rating the performance of propulsion systems, it is the usual practice to indicate the power available for reciprocating engines and the thrust available for jet engines. Thus, for a jet-propelled aircraft, the maximum flight speed is estimated easily by superposing a plot of thrust available on the thrust-required curve, as calculated in Eq. 9.9. The intersection of the two curves indicates graphically the point at which the available thrust is exactly equal to that required for level flight. The corresponding speed represents the maximum flight speed.

Equivalently, we equate the expression for the thrust available (usually a func­tion of speed) to the thrust available and then solve for the corresponding speed. In carrying out this calculation, it is necessary to use a model of the propulsion-system performance as a function of flight speed. A manufacturer of a system usually pro­vides these data to an airframe designer.

To estimate the maximum flight speed for a reciprocating-engine propulsion system, it is most useful to work with power instead of thrust. We accomplish this in the next subsection and illustrate results for the Bf-109G.

Power Required for Level Flight

Recalling that power is the rate at which work is done and that the work done by an engine is the thrust force times the distance traveled, then the power required for unaccelerated, level flight is:

(9.14)

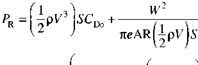where V is flight speed. Using Eq. 9.9, we find:

(9.15)

This expression is plotted in Fig. 9.5 for the example airplane at two altitudes (i. e., sea level and 22,000 ft) to illustrate the effect of atmospheric density on the results.

Figure 9.5. Power required for Bf-109G.

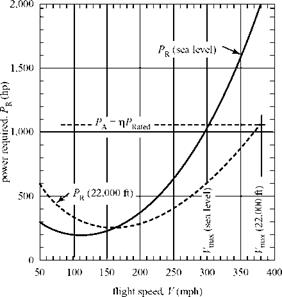Notice that at low speed, the power required is higher for the high-altitude case, whereas for high speeds, the opposite is true. This is due to of the parasite-drag penalty that dominates in the high-speed range. The effect of the induced drag becomes much smaller at high speeds, as indicated by Eq., 9.15. Therefore, the higher density for the low-altitude case results in more power required at a given flight speed.