Navier-Stokes Flow

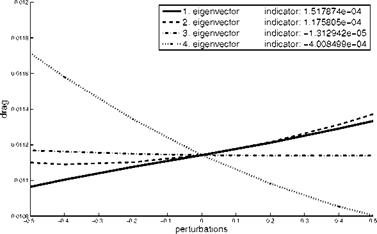
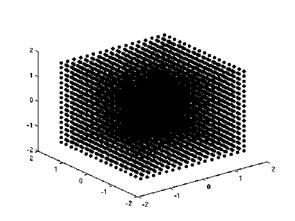
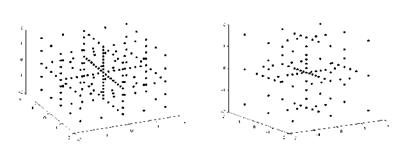
As in the Euler case, we investigate the influence of the individual eigenvector of the Karhunen-Loeve expansion on the target functional depicted in Fig. 18 Since the third eigenvector has no impact on the target functional, the mean value is ap­proximated using the first, second and fourth basis vector (cf. (75)). If the same error tolerance 3 • 10~4 as in the previous testcase is required, a full grid of 4913 grid points based on multilinear ansatzfunctions has to be used in order to compute the objective function. A reduction factor of 28 can be achieved by a sparse grid approach which is further improved by a local refinement strategy. The resulting adaptive grid consists of 99 grid points.

Since the computational effort in the Navier-Stokes case is much higher than in the Euler testcase, the number of grid points need to be further reduced in order to make a robust optimization possible. The use of Gaufi-Hermite quadrature formulas results in the same full grid and sparse grid shown in Fig. 13 and Fig. 14 as in the Euler testcase fullfilling the error tolerance 3 • 10~4. The dimension adaptive approach leads to the following grid 21.

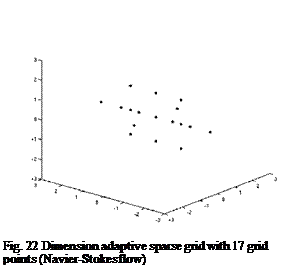
The linearity of the drag depending on the first eigenvector (cf. 18) is recognized by the dimension adaptive algorithm, so that this dimension is not further refined. Since the linear behaviour might change during the optimization, we add two points ensuring that the first eigenvector is taken into account during the optimization, see Fig. 22. Fig. 23 and 24 illustrate the drag and lift performance of the 17 perturbed geometries of the single setpoint and robust optimization.

The mean value of the drag in the robust case is a little bit higher than the mean value of the single setpoint optimization (5 drag counts) which can be attributed to the lift constraints. The robust optimization is feasible over the whole range of

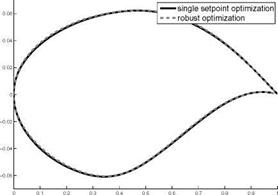perturbations as required, whereas the single setpoint optimization cannot reach the target lift in more than 60 % of the realizations. Hence, we can state that the semi­infinite optimizations leads to a better lift to drag ratio as in the Euler case. The resulting shapes are depicted in Fig. 25. The difference between the robust shape and the single setpoint optimized shape is smaller than in the Euler case, indicating that the profile is more sensitive to changes of the shape.