Normal Form of a Plane

The definition of a plane by Eq. (2.23) may be somewhat intimidating for its complexity. There exists an alternate, simpler formulation, which is also quite useful for modeling planes. It is called the normal form because the unit normal vector defines its orientation.

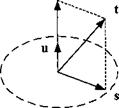
Let the unit normal vector of a plane be given by и (see Fig. 2.17). Premultiply­ing Eq. (2.23) by the transpose of и generates scalar products on both sides of the equation

US HR = uUSfjBa + vus vb„ + us B0R

Because и is orthogonal to sub0 and svb„- the first two terms on the right-hand side

are zero; and, with sb„r being constant (see Fig. 2.17), we have the condition for В to sweep out the plane: usBR = const.

Definition: A plane, with unit normal direction u, is defined by the sweeping

point В, referred to point R, such that the scalar product of the two vectors is constant

usBR = const

In your pursuit of modeling planes, you may wonder which definition is appropriate for your situation. Here are the telltales: If the plane is given by points or embedded vectors, use Eq. (2.23), otherwise apply Eq. (2.24) with the unit normal vector.

Example 2.7 Angle Distance Measuring

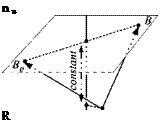
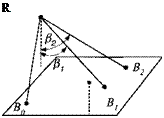
Problem. An aircraft R with an INS and distance-measuring equipment on­board is to determine the distances to points B and Вт, given its own known displacement vector sBoR (see Fig. 2.18). All three points lie on the surface with unit vertical vector u, established by the INS. The sensor of the distance-measuring equipment, however, can only measure the angles and fij between the local ver­tical and the direction to the points. Derive the equations that calculate the two distances sBir and |sB2*|.

Solution. Because all three points lie on the surface, we have from Eq. (2.24) the relationships

usBoR = usBlR = usBlR = const

The first term is given and establishes the value of the constant. The scalar product of the remaining terms can be expressed in terms of the length of the vectors and their angles from the vertical

|5BlS|cOs/Ji = |іВ2я| COS/S2 = const From which we obtain the desired lengths

const

cos fa

r Fig. 2.19 Plane projection.

This is a typical application for the normal form of a plane. The unit vector of a plane is a free vector in accordance with the characteristics of a plane as a two-dimensional manifold. The free parallel displacement of the vector и in two dimensions corresponds to the two parameters и and v of the original definition, (Sec. 2.3.3).