Projectiles and satellites

Among the many assumptions so far made one of the most impracticable has been the idea of leaving the earth’s surface at speeds of about 11 km/s.

But we all know the answer to this problem now, and it lies in rocket propulsion; by this means the acceleration is so comparatively gentle that it can even be withstood by human beings, at any rate in the lying down pos­ition.

When we consider the use of rockets to propel bodies to great heights or into a space a new complication is introduced in that owing to the great rate of fuel consumption the very mass of the projectile decreases rapidly, so we have the double effect of mass decreasing with fuel consumption and weight decreasing with distance from the earth. Moreover, in multi-stage rockets, which are the only practical means of achieving the velocities required for launching into space, there is a further decrease in mass each time a stage is completed and a part of the rocket is detached. The final mass that becomes a satellite, or goes off into space never to return, is but a small fraction of the mass at take-off.

In the interests of fuel economy turbojets, or better still ramjets, may be used for the flight of projectiles while they pass through the earth’s atmosphere, but in space rockets are the only means of powered propulsion, and all jour­neys in space are dependent on rockets and the law of universal gravitation.

In order to get our ideas straight we have so far considered the motion of missiles in a straight line – straight up and down from the earth’s surface. We did the same thing in Chapter 1 in dealing with ordinary mechanics, but then we graduated to the much more interesting motion on curved paths; this is what we are going to do now.

What happens if instead of throwing the stone vertically we throw it hori­zontally? – still neglecting the effects of air resistance.

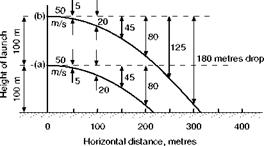
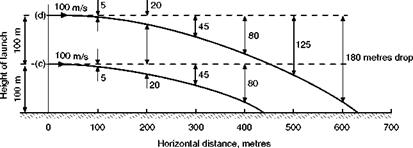
It will start with no vertical velocity, but will immediately begin to acquire a downward velocity at the rate of roughly 10 m/s2 – meanwhile it will retain its horizontal velocity. After 1 sec it will have fallen about 5 m, after 2 sec 20 m, and so on. If its initial horizontal velocity was 100 m/s, and if it was launched from a height of 30 m, its path of travel would be something like (a) in Fig. 13.3, or if it was launched from twice the height, like (b). If its initial horizontal velocity was 200 m/s, its path of travel would be more like (c) or (d) respectively.

It will be quite clear from these figures that the distance it will travel over the ground before striking the ground depends on the height at which it is pro­jected, and the horizontal velocity with which it is projected (the velocity being more important than the height). If it is projected at ground level it won’t get any distance before hitting the ground whatever its horizontal velocity; on the other hand, if it is projected from considerable height, and at a considerable horizontal velocity, it will travel a considerable distance horizontally before reaching the ground. The path of flight, or trajectory, is a mathematical curve called a parabola.

But now we have been guilty of making yet another assumption – has the reader noticed it? In the figures, and in our reasoning, we have assumed that the earth is flat. Not just that it is free of hills and dales (these won’t affect its flight path but they may obviously affect the point at which it hits the ground), but that the earth is itself a flat plane instead of being spherical or very nearly so. Such an assumption has no practical significance in the flight of stones or

Fig 13.3 Bodies launched horizontally – paths of flight
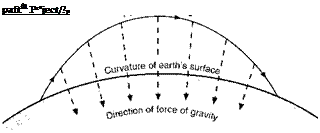
cricket balls – but is all-important in the flight of high-speed projectiles. The curvature of the earth will affect the path of the projectile, and the distance it travels before striking the ground, for two reasons – first, because if the pro­jectile didn’t ‘fall’ towards the earth it would go off at a tangent and so get farther and farther away; secondly, because although the force of gravity acting on the body is always ‘vertical’ in the sense that it is always towards the centre of the earth, the direction of the vertical will change in space and this will change the shape of the curve – in mathematical terms it means that the trajectory is an ellipse rather than a parabola. These effects are shown in the figure (Fig. 13.4) – hopelessly exaggerated of course in the case of a stone or cricket ball, or even an ordinary shell fired from an ordinary gun, but not by any means exaggerated for modern rocket-propelled high-speed ballistic mis­siles and not, in this figure, even going as far as the man-launched satellite or space-ship.

It should now be clear that the greater the speed with which a projectile is launched from a given height above the earth’s surface in a horizontal direc­tion, the larger will be the curve it describes and so the greater will be the distance it travels before it hits the surface; in other words, the greater will be the range.

The actual range, of course, depends on the direction of launch as well as the speed and height but at first it is easier to consider only horizontal launches. And by ‘launching’ we mean that the projectile is given a velocity and then left to itself – and so becomes subject to the mechanics of ballistics. If it continues to be rocket-propelled almost anything may happen!

If we take ‘launch’ to have this meaning, then the launch conditions can be achieved at the end of the ‘launch cycle’ involving, usually, rocket propulsion between the earth’s surface and the launch point where the rocket is switched off and the body left to the mercy of ballistics.

Tet us assume then that we are launching a projectile horizontally from a height of 800 km above the earth’s surface. This besides being a nice round figure is well outside any appreciable effects of the earth’s atmosphere, and although it is even farther beyond the ceiling of ‘aeroplanes’ it is within the reach of multi-stage rockets. To those of us who are accustomed to think of heights in thousands of feet or metres it sounds a great height (eight hundred

Fig 13.4 Path of projectile – curved earth

thousand metres), but in terms of space travel it is practically nothing, only one eighth of the radius of the earth away from the surface, about one four hundred and eightieth of the distance to the moon, and one hundred thou­sandth of the distance to the sun. At this height the weight of a body and the acceleration due to gravity are reduced by about 20 per cent of what they were at the earth’s surface.

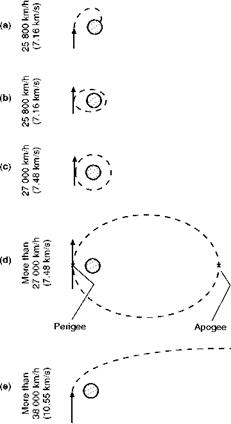
So much then for conditions at our launching platform, let us now see what happens as we increase the velocity of a horizontal launch. At first the projec­tile will simply get farther and farther round the earth, but always coming down to earth again at some point less than half way round (Fig. 13.5a, over­leaf). Then at a certain velocity (about 7.16 km/s or 25 800 km/h) a most exciting thing will happen (or at least it would happen if it were not for our old enemy air resistance) – the projectile will just miss the surface on the far side of the earth and will then gain height again, and, perhaps most exciting of all, will circle the earth and come round to where it started – and will then repeat the performance – and so on. The projectile has become a satellite – it is travelling round the earth under its own steam as it were (Fig. 13.5/?).

Unfortunately it can never happen quite like this because although it was clear of air resistance at the launch, on the far side it would have come right through the atmosphere to ground level and so would burn up owing to the heat created or, even if it could be shielded in some way from this, it would lose speed and fall to the earth.

But we have only got to increase the launching velocity a little further and the projectile will then miss the far side of the earth by an appreciable margin, and when this is say 300 km, it will miss most of the atmosphere and so con­tinue to circle the earth on an elliptical orbit, clearing it by 800 km on one side and 300 km on the other – in any such orbit the point at the greatest distance from the centre of the earth is called the apogee, and the point nearest the centre of the earth the perigee. Our projectile is now a practical satellite – prac­tical, but still not very probable.

Even at a height of 300 km there is some atmosphere, and there probably is even at 800 km for that matter, so this satellite will lose speed every time it dips into the atmosphere, and so will gradually lose the energy given to it at the launch and will sooner or later come down to earth on a spiral path.

But we need not be disheartened, because a further increase of launching speed will further increase the clearance on the far side, and so gradually elim­inate this problem until, at a launching speed of about 7.48 km/s we reach another interesting stage at which the satellite – we can no longer call it a pro­jectile – travels round the earth on a circular path, 800 km from the earth’s surface, and there is no longer any distinction between the apogee and the perigee (Fig. 13.5c). The launching speed at which this occurs is called the cir­cular velocity.

After this long story the reader will probably be able to guess what happens with further increase of launching speed. Yes, the circle again becomes an ellipse but the apogee, or farthest point, is now on the far side of the earth and

Fig 13.5 Earth satellites

Speeds refer to horizontal launches from 800 km above the earth’s surface, in the interests of clarity this distance has been exaggerated in comparison with the radius of the earth.

the perigee is the point of launch (Fig. 13.5d). Still further increases of speed make the ellipse more and more elongated with the apogee getting farther and farther from the earth. It will not be difficult to understand why this type of orbit is frequently used; it practically eliminates the problems of air resistance, it is not dependent on an exact launching speed and it allows scope for travel at the apogee to great distances and so, for instance, for passing beyond the moon or other planets, or hitting them.

Is this the end of the story? Not quite. Strange as it may seem the ellipse cannot be stretched indefinitely, and at a launching speed of about 10.7 km/s – different speeds at different heights – the ellipse becomes an open curve, a parabola, and the satellite travelling on this open curve escapes from the earth for ever, and becomes a satellite of the sun (Fig. 13.5e). Yes, this is the escape velocity again, and it only differs numerically from the previous one because we are now launching from 800 km instead of from ground level. So the escape velocity is the highest velocity at which a body can be launched in any direction and be expected either to orbit the earth or return to it again – above that speed, speaking vulgarly, we have had it. Above that speed, too, the path of travel changes from a parabola to a different open curve called a hyperbola, but this is a subtle change for a subtle reason, and it need not worry us.

This is not quite the end of the story as at even higher speeds there comes a point where the object can escape from the solar system and carry on out into space indefinitely.