Reference Frames

Without reference points and frames we could not model positions or motions of aerospace vehicles. Reference frames in particular have captured the interest of astronomers over millenniums. Just recall the argument whether the Earth, the sun or the stars should constitute the primary reference. In recent times, the launching of satellites and interplanetary travel of spacecraft have made it a matter of prac­tical importance to clearly understand reference frames and coordinate systems. Vallado1 gives an up-to-date account in his book Fundamentals of Astrodynamics and Applications.

We will concentrate on those frames that are of primary importance for the modeling of aerospace vehicles. The Sun-centered (heliocentric) frame serves all planetary space travel, whereas the Earth-centered frame suffices for Earth satellite trajectory work. Both are considered inertial frames in the Newtonian sense; the choice depends on the application. For Earth-bound flights the rotation of the Earth can often be neglected. Under these circumstances the Earth frame itself becomes the inertial reference. Even the vehicle’s body can become a reference frame for rotating turbine blades, propellers, or gimbaled seeker heads. We shall define these frames now in detail using the concept of base point and base vectors.

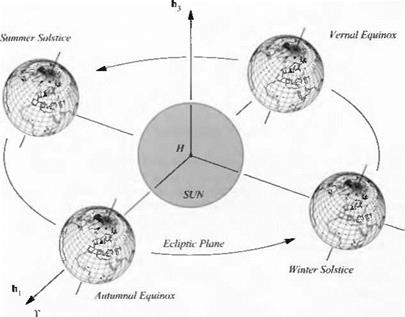
3.1.2.1 Heliocentric frame. For all of humanity the sun is the major frame of reference. It separates day and night, the seasons, and the years. It is the main source of energy, and its gravitational pull keeps the Earth and the planets on their

Fig. 3.4 Heliocentric frame of reference.

elliptical paths. As the Earth revolves around the sun in one year, it encircles the ecliptic plane. The astronomers speak of the mean ecliptic, which averages some minor periodic fluctuations. Because the Earth is tilted about 23.5-deg from the ecliptic, we experience the four seasons. Figure 3.4 visualizes the yearly cycle for you.

The sun is not solid but gaseous and possibly liquid. In the midst of all of the explosions, there are no reference points mutually at rest; therefore, we have to create them artificially. We pick the gravitational center as the base point H. The third base vector A3 is normal to the ecliptic, pointing upward, based on the Earth’s orbital direction and the sense of the vector abiding by the right-hand rule. We need at least one more base vector to fully define the triad (the third one follows from the orthonormal condition). The choice is the first base vector h, which points to the First Point of Aries; or at least where the star constellation was during Christ’s lifetime. Today it points in the direction of the constellation Pisces.

How is that direction defined? At the first day of spring (vernal equinox), position yourself at the center of the Earth. As you look out, you see the intersection of the equator and the ecliptic lining up with the sun. If you had been bom 2000 years ago, you would have seen the constellation Aries beyond the sun—an impossible feat with human eyes. The sign indicating Aries is a modified Greek T, resembling a ram.

Summarizing, the heliocentric frame is modeled by the base point H and the three base vectors h,h2, and й3, with h 1 pointing to T, й3 being the normal of the ecliptic plane, and h2 completing the triad. If you ever get to travel to Mars, you

Fig. 3.5 Inertial reference frame.

would become very familiar with this heliocentric frame. However, back at planet Earth, even as astronaut of the International Space Station, you would more likely be dealing with the geocentric-inertial reference frame.

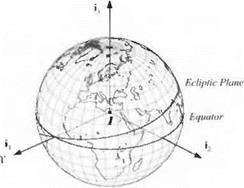
3.1.2.2 Geocentric-inertial (J2000) frame Now let us concentrate on the Earth as we view it in Fig. 3.5. The most useful inertial frame is collocated with the center of the Earth, but its orientation remains fixed in the ecliptic. This is a good example of why we have to distinguish between location and orientation of a frame. The location of the frame is given by the displacement vector Sm of the center of the Earth I wrt the center of the sun H. Its orientation is described by the base vectors i’i, t’2, and 13.

To define the vector i’i, we have to carry out a Gedanken experiment (“Gedanken” is German for “thought”). Imagine a nonrotating shell around the Earth with the etched trace of the equator. The ecliptic, projected on the shell, is the path of the sun during one year. It will intersect the equator at two points. Of particular interest is the point when the sun crosses the equator in spring. This point is called the vernal equinox, already introduced in Fig. 3.4. We align with this direction the first base point *1. It points at the constellation Aries and therefore is fixed with the stars. The remaining two base vectors are easily defined. The Earth’s axis of rotation serves as direction and sense for І3, and t’2 completes the right-handed triad.

Unfortunately, the equatorial plane, just as the ecliptic and the axis of rotation, moves very slightly over time. We can only speak of a truly inertial frame if we refer to its position at a particular epoch. Therefore, the astronomers defined the J2000 System that is based on the Fundamental Katalog, FK5.1 This system is the best realization of an ideal inertial frame. It is the foundation for all near-Earth modeling and simulation. We will therefore refer to it just as the inertial frame.

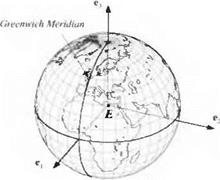
3.1.2.3 Earth frame. Look around you and take notice of the Earth (see Fig. 3.6). Its particles form the Earth’s frame. The base point E is at the Earth’s center, and the triad consists of the base vectors e , e-i, and £3. One meridian of the Earth assumes particular significance. It is the prime meridian that traces through the Royal Observatory at Greenwich, a suburb of London. Its intersection with the

Fig. 3.6 Earth frame.

equator establishes the penetration point of the first base vector e. The Earth’s axis of rotation serves as the direction and sense for the third base vector Є3, and Є2 completes the triad.

The prime meridian serves as origin for measuring longitude (positive in an easterly direction), whereas latitude is surveyed from the equatorial plane (positive in northerly direction). These reference lines are fixed on the Earth and ideal for locating sites on the Earth’s surface.

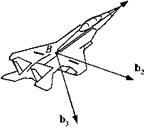
3.1.2.4 Body frame. Aircraft, missiles, and spacecraft are of primary con­cern for us. If they can be considered rigid bodies, they are represented by a frame, the so-called body frame. Although this frame is usually not used as a reference, it is nevertheless important for modeling location and orientation of vehicles under study. Its base point В coincides with the c. m., and the base vectors b,b2, and Ьз are aligned with the principal axes of the moment of inertia tensor.

Sometimes other directions are more relevant. For instance, the b vector for an aircraft is more likely aligned with some salient geometrical feature, like the tip of the nose or the zero-lift line at a particular Mach number (see Fig. 3.7). The aircraft designer has even adopted the terminology of his colleague, the ship architect, and calls it the waterline. However, for all vehicles bj is parallel to the second principal moment of inertia axis.

b,

Table 3.1 Summary of frames Frame Base point Base vectors First direction Third direction Heliocentric H center of sun huh2,h3 h Aries A3 normal of ecliptic Inertial I center of Earth in *2, Із ii vernal equinox i3 Earth’s spin axis Earth E center of Earth Є, e2, е3 Єї Greenwich e3 Earth’s spin axis Body В center of mass bu b2, b3 bi nose A3 down

For aircraft, the positive sense of the b base vectors is out the nose, bj out of the right wing, and b3 down, completing the triad. For missiles with rotational symmetry, any direction for b2 and Й3 is a principal axis. Therefore, control fins or geometrical marks may be used to fix them.

If elastic phenomena need be modeled, a body frame is still required as a ref­erence for the bending and vibrating modes. This frame could be defined as co­inciding with the vehicle under no-load conditions; or, in the case of wing flutter, the fuselage alone could be chosen. Sometimes the whole vehicle is divided into many rigid body subframes, and one of them is chosen as the primary reference.

3.1.2.5 Summary. In this section I have introduced four important frames. Starting first with the heliocentric frame of reference for interplanetary travel, then zeroing in on the geocentric inertial frame for orbital trajectories, we eventually come down to Earth to define the Earth frame, which serves as reference for most atmospheric flight. In addition, the body frame is of particular significance. It models the position and orientation of the vehicle, which we want to simulate.

Table 3.1 summarizes the four frames. Notice the significance of the ecliptic and the equatorial planes. Their normal unit vectors define the direction of three base vectors (the Earth’s spin axis is normal to the equator). You may be puzzled by the fact that the center of the Earth is the base point for both the inertial and the Earth frames. Indeed they coincide. Of all the points of the Earth frame, the center is the only point shared with the inertial frame.

You probably cannot wait any longer to meet the more familiar coordinate systems. Their time has come. I only hope that you keep in mind their fundamental difference with frames.