Scalar Product

If the transpose of vector* is multiplied with the vector y, we obtain a scalar

xy = scalar

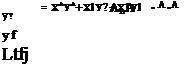This is the scalar product of matrix algebra. For any coordinate system ]A the scalar product is

If multiplied by itself, the resulting scalar is the square of the vector’s length. For any ]A

[x]A[x]A = (xf)2 + (xA)2 + (xA)2 = x2

Because the scalar |x[2 is invariant under coordinate transformations, this statement holds for all coordinate systems

** = |x|2 (2.14)

What is the form of the scalar of Eq. (2.13)? Consider the vector triangle of Fig. 2.6. From the law of cosines, the squares of the length of the three vectors are related by

z2 = {x2 + |y|2 – 2|x||y| cos#

On the other hand, z2 is also obtained from the scalar product of the vector subtraction z = x — у

z2 =zz = (x-y)(x – y)

= XX +yy – yx – xy

= x2 + |y|2 — 2xy

Comparing the last equation with the law of cosines furnishes the value for the

scalar. The scalar product is therefore

= [jc||yicos6* (2.15)

The scalar is x times the projection of у on x and assumes the sign of cos в. In Eq. (2.15) we can exchange the symbols without changing the result; therefore

xy = yx

However, beware of moving the transpose sign. The result is xy Ф xy (why?).

Example 2.1 Angle Between Two Beams

Problem. A traffic control radar R tracks two aircraft A and В and records their displacements in geographic coordinates ]G as [їдя]° = [20 10 —9] and [srkg = [30 —20 —9] km. What is the angle between the two radar beams?

Solution. Solve Eq. (2.15) for в

1‘SakII‘SBkI /

substitute the matrices and multiply out

( [20 10 —9][-lo] ^

У202 + 102 + (-9)У302 + (-20)2 + (—9)2

V