Straight Line

Straight lines arise as models of straight trajectories, star sightings, surveying of landmarks, or just a person walking down the aisle of an aircraft. They are considered of infinite length, but contain a displacement vector, whose endpoint moves along the line.

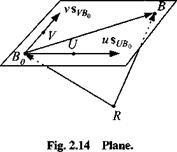
We let the point В slide along the straight line, starting from an initial point Bo, while maintaining R as a fixed reference point (see Fig. 2.12). The sliding process is generated by a scalar parameter и, e: — oo < и < +oo that lengthens or shortens the vector sBb0 ~ usUHt, on the line. The vector sub0 establishes the direction of the line and could be a vector of unit length.

Definition: A straight line, with direction sUB„ and anchored at sBoR, is defined

by the sliding of point B, referred to point R

Sbr = USuB0 + Sfl0«

The line is a one-dimensional manifold with parameter u.

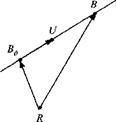It takes three extra points to describe the sliding of point В: the reference point R and the two points U and B0> which establish the direction of the line. If the reference point should be on the line, B0 could assume its function.

Fig. 2.13 Flight line.

Example 2.5 Straight Line Trajectory

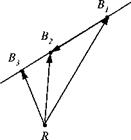
Problem. A surveillance radar R took two fixes of an incoming attack fighter: [ї]+к]с = [30 10 —8] and [лЙ2Й]с — [20 —5 —6] km (see Fig. 2.13). Timing the two fixes gave an elapsed time of At = 50 s.

1) Determine the average speed of the aircraft.

2) Where will the aircraft be ([5b^r]g) after Дт = 20 s has elapsed beyond Bj. assuming it continues its steady and straight flight?

Solution. 1) The speed of the aircraft V is calculated from the distance |.уЙ2Й| | divided by time

[^І7]С = [^f – [Si^f = [-Ю -15 2]

V = = — = 0.3628 km/s = 362.8 m/s

At 50

2) Because the aircraft flies along a straight line, its displacement after 20 s from the radar station is according to Eq. (2.22)

[■Sfi3«]G = + [sBi/f]

where Іл’й, й| ]G points in the direction of flight. The parameter и is calculated from the time ratios

At

then the radar will pick up the aircraft after 20 s at [Sb^]G = 1.4 x [-10 -15 2]+ [30 10 -8] = [16 -11 -5.2] km

The parameter и in this example is actually a time ratio, which occurs quite often in these types of problems.