The mechanics of circular orbits

So much for the story of what happens – what is the explanation of it all? In the particular case of the circular orbit the satellite is very like a stone on the end of a string stretching from the centre of the earth to the satellite; the satel­lite is all the time trying to go off at a tangent but is being given an acceleration towards the centre by the centripetal force which is of course the force of gravity. So, near the earth’s surface, if we neglect air resistance, the centripetal force will be the weight of the satellite, and the acceleration towards the centre will be 9.81 m/s2. Notice that a body circling the earth is accelerating towards the centre at the same rate as a body falling straight towards the earth. So we can easily calculate the circular velocity near the earth’s surface because the acceleration = v2lr (see page 14).

Now r is the radius of the earth, say 6370 km (6 370 000 m), so v2lr = g, i. e. iP-!6 370 000 = 9.81

Vі = 62 490 000 v = 7905 m/s = 7.9 km/s approx = 28 440 km/h approx

How long will the satellite take to make a complete circuit of the earth at this speed?

Circumference of earth = 2.к X 6370 km

So time of circuit at 28 440 km/h

= (2n X 6370)/28 440

= 1.41 hours or about

1 hour 25 minutes

It will be noticed that the circular velocity we have calculated, i. e. 7.9 km/s, is higher than the circular velocity at 800 km from the earth’s surface, i. e. 7.48 km/s; but there is no mystery in that and we can easily work it out for our­selves by replacing the earth’s radius of 6370 km by 7170 km, and reducing g by 20 per cent, i. e. to about 7.85 m/s2. The value of v1, and so of v, will then be less because whereas the value of g is reduced by 20 per cent, the value of r is only increased by 12y per cent – this, in turn, is because the value of g depends on the force of gravity, which is inversely proportional to the square of the distance r.

And what will be the time of a complete circuit at 800 km from the earth’s surface? The distance is greater, the speed less, so the time of orbit will be greater. Work it out and you will find that it is about 1 hr 40 min. Similarly at 1600 km the circular velocity is about 6.9 km/s and the time of orbit nearly 2 hours.

A distance of 35 400 km from the earth gives a particularly interesting cir­cular orbit because the time of a complete circuit is 24 hours; so a satellite travelling at this speed – in the right direction, of course – remains over one spot on the earth; a communication satellite such as is used for transmitting TV and radio signals from one part of the earth to another.

Then at about 385 000 km the circular velocity is a mere 3700 km/h (just over 1 km/s), and the time of orbit 28 days – but on that circuit we already have a satellite that surpasses in many ways any so far launched by man – the moon.

And now we can answer an obvious question – why doesn’t the moon fall on to the earth? Because it is revolving round the earth at just such velocity and radius that the centripetal force is provided by the gravitational attraction, in other words, in a sense it is ‘weightless’ – and this applies to all those bodies in orbit, whether circular or not, and to all the people and things inside them. Strictly speaking they are not weightless at all; in fact it is their weight, the force of attrac­tion between them and the earth (or moon) which they are orbiting, that keeps them in orbit and prevents them from going off at a tangent. They merely seem to be weightless, and that is why a man can get out of a space-ship while in orbit, and continue in orbit himself, just like the space-ship, without any fear of ‘falling’ back to earth or to anywhere else. Although he may be travelling at several kilometres per second he has no sense of speed, and apparently no weight – he just floats, and has no difficulty in keeping near the space-ship which is also just floating! More correctly the man, and the space-ship, and all the other things in orbit, are falling freely, are accelerating towards the earth because of the attraction of the earth – in short because of their weight – so much for weightlessness! In the same sense the moon is falling towards the earth, though it never gets any nearer!

Notice that the reader can calculate all these circular velocities and times of orbit for himself, including that of the moon. For at all distances from the centre of the earth, the condition for a circular orbit is that the acceleration towards the centre shall be the ‘g’ or acceleration of gravity at that distance; this we might call gd, and it must be equal to v2ld.

But gd is also proportional to the force of gravity, which is inversely pro­portional to the square of the distance.

Since at the earth’s radius r, the acceleration is g,

gd will be g X r2/d2

Therefore for circular velocity at any distance d, v2!d = g X r2/d2 i. e. v2 = gr2/d.

Figure 13.6 (overleaf) shows circular orbits at different distances from the centre of the earth.

It shows how a whole system of bodies can circle the earth, of their own free will as it were (once they have been put in orbit), and how the farther out the orbit the slower is the speed. It rather reminds one of the way in which Sir James Jeans once described the solar system as being like the traffic in Piccadilly Circus, with ‘the traffic nearest the centre moving fastest, that farther out more slowly, while that at the extreme edge merely crawls – at least by comparison with the fast traffic near the centre.’[10] But there is an important distinction between the solar system – the work of nature – and bodies orbiting the earth – the work of man (except for the moon); in the solar system, again to quote Sir James Jeans, there is only ‘one-way traffic’, and the orbits of the planets round the sun are mostly circular, or very nearly so, whereas the man-made satellites orbit the earth in various directions and, as we shall soon discover, some of their paths are very far from circular.

When talking of the interesting possibilities of a 24-hour circuit we men­tioned the direction of rotation. This would be all important in this case because if the satellite was rotating round the equator in the same direction as the earth’s rotation it would stay over the same spot on the earth’s surface but if it was travelling in the opposite direction – well, what would it do? Would it go twice round in a day? or would it merely appear to do so? or what?

But the fact that the earth is rotating will of course affect all launches, because it means that we are launching from a moving platform. The surface of the earth at the equator is travelling at a speed of rather over 1600 km/h owing to the spin of the earth on its axis, so a body launched in the same direc­tion, i. e. towards the east, will already have the advantage of this speed and so will need 1600 km/h less extra speed to achieve circular velocity, escape vel­ocity, or whatever it may be. Towards the west it will need 1600 km/h more extra speed. There can also be circuits of the earth in other planes altogether,

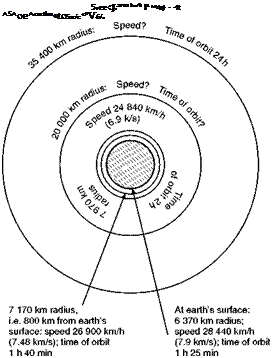Fig 13.6 Circular orbits at different distances from centre of the earth Note. The speed at 35 400 km radius, and the speed and time of orbit at 20 000 km radius, have been left for the reader to work out for himself.

e. g. over the poles, and in these cases the effect of the earth’s rotation on launching and orbiting is more complicated.

It is not always realised, and it is interesting to note, that since the earth’s surface at the equator is travelling at about 1600 km/h all bodies on the earth are in a sense trying to be satellites, and to go straight on instead of following the curvature of the earth. Thus there are two reasons why a body of the same mass weighs less at the equator than at the poles, first because it is farther from the centre of the earth so the true gravitational attraction is less, and secondly, because a proportion of the gravitational force has to provide the centripetal acceleration. How much is this centripetal force? Is it appreciable? Well, work it out for yourself. Take the actual velocity as 1690km/h, the radius of the
earth as 6370 km, g as 9.81 m/s2, and you will find that the centrifugal force on a mass of 1 kg is about 0.018 N.