Vector Product
Let us ask another question: What kind of multiplication of two vectors x. у yields a vector z? From matrix algebra we know that a 3 x 1 vector is only obtained by the multiplication of a 3 x 3 matrix with a 3 x 1 vector
1Х][у] = И (2.16)
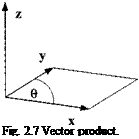
We want to explore the form of [X]. Vector algebra gives us three conditions for a vector product, as visualized by Fig. 2.7:
1) z normal to x and y.
2) |z| = area of x and у parallelogram.
3) right-handed sequence: x —> у —*■ z.
 |
These conditions will lead to the conclusion that [X] is the skew-symmetric form of x 1:
|
■*f |
A |
‘ 0 |
-*3 |
X2~ |
|
|
MA = |
*2 |
O [X]A = |
*3 |
0 |
-X; |
|
_*3_ |
_~*2 |
Xl |
0. |
for any allowable coordinate system ]A. Therefore, the vector product in tensor algebra is expressed by
Xy=z (2.17)
with the understanding that X is the skew-symmetric tensor of x.
Proof: If X is skew-symmetric, it satisfies the three conditions of the vector
product:
1) The first condition consists of two orthogonality conditions, a) For z to be normal to x, their scalar product must be zero: zx = 0; with Eq. (2.17) yXx — 0, which is satisfied if Xx = 0 . This is indeed the case as demonstrated by the matrix multiplication (for any ]A)
|
0 лгз — xf |
A |
~xf |
A |
X3X2 – X2X3′ |
A |
-СГ |
|
—хз 0 X |
Xl |
= |
-X3XI +XIX3 |
= |
0 |
|
|
X2 —X 0. |
Хз. |
X2X1 — XX2 |
0 |
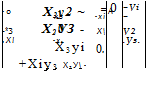 |
|
b) For z to be normal to y, their scalar product must be zero: zy = 0; with Eq. (2Al)yXy = 0, which is satisfied if X is skew-symmetric
The matrix multiplication holds for any allowable coordinate system. Therefore, if X is skew-symmetric, so is X, and the first condition is satisfied.
2) The second condition requires that the length of vector kl = area of the parallelogram subtended by the vectors* and y. Let us express Eq. (2.17), with X as a skew-symmetric matrix, in an arbitrary coordinate system ]A.
|
~Zl |
A |
– 0 |
-*3 |
X2 |
A |
"Tf |
A |
■~*зУ2 + ТгУз- |
|
Z2 |
= |
*3 |
0 |
X |
У2 |
= |
*ЗУі – *іУз |
|
|
.гз. |
. x2 |
X |
0. |
-Уз. |
_-*2Уі +Хіу2_ |
|
The scalar product of z with itself is the square of its absolute value [z}A[z]A = z2 = z + zl + z] |
= (Х2уъ – ХЪу2)2 + (*ЗУі – ХіУз)2 + (хіУ2 – Х2у)2 = (х2 +х+ х|)(у2 + у + Уз) – (ХіУі + Х2У2 + *зУз)2 The last line can be written as
kl2 – w2|y|2 – ([X][y])2 = M2|y|2 – |x|2|y|2cos2в = |x|2|y|2(l – cos26») Replacing (1 — cos2 в) = sin2 в and taking the square root yields
kl = kllyl sin#
which is the area of the parallelogram between vectors x andy. By choosing for X the skew-symmetric form, we have indeed satisfied the second condition of vector multiplication.
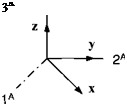
3) The third condition states the right handedness of the vector product. Let us introduce a right-handed Cartesian coordinate system Iа, 2A, and 3A. For the particular situation in Fig. 2.8, the vector product assumes the form
|
– 0 |
0 |
х2- |
л |
"0" |
А |
– о – |
|
0 |
0 |
-Х |
У2 |
— |
0 |
|
|
–Х2 |
Хі |
0_ |
0 |
_*1.У2_ |
|
[zf = [X]A[y]A |
|
If x and у2 are positive, so is гз – Therefore, the skew-symmetric form of [X] satisfies the right-handedness condition as demonstrated by this specific example. |
 |
We have indeed confirmed that the vector product of two vectors x and у consists of the multiplication of the skew-symmetric form of vector x with vector y. In coordinate form we execute a matrix multiplication.
I introduced vector multiplication in a simplified form, adhering to vector mechanics rather than to tensor algebra. The right-handed convention eliminates the need for third-order tensors, which are really required to define the vector product properly. For the theoretically inclined among you, I provide the tensor definition of a vector product. Let, v,, and zk be three vectors in Euclidean space, and c, jk the third-order permutation tensor, then the vector product is defined (dummy indices summation implied):
Zi = SijkXjyk
It is valid for any type of coordinate system compatible with the Euclidean metric. By agreeing to use only right-handed Cartesian coordinate systems and the right – hand rule of vector products, we can use the simpler Eq. (2.17) as a definition of the vector product. You will see that this version is adequate for modeling all situations related to aerospace vehicles.
Example 2.2 Area Calculation
Problem. A farmer’s son inherits a rhombus-shaped field (Fig. 2.9). The bam is located on the corner B. With a global positioning system (GPS) set he records the coordinates of В and the two adjacent comers C and D. Then he converts the data to two vectors in geographic coordinates [,?celG = [0.5 2 0] and sdhg = [2 0.5 0] km. How many square kilometers of land did he inherit?
Solution. Apply Eq. (2.17) and take the absolute value of the cross product to obtain the area A:
A = |[SCB]Gto»]G|
where Schg is the skew-symmetric form of [s’cel0-
|
Г 0 |
0 |
2 – |
– 2 – |
‘ 0 "I |
|
|
0 |
0 |
-0.5 |
0.5 |
— |
0 |
|
L-2 |
0.5 |
0 |
0 |
-3.75J |
Notice, there was no need for a coordinate system origin.
2.2.5.1 Vector triple product. For any three vectors x. y. andz with X and Y, the skew-symmetric forms of x andy, the vector triple product, is defined as
XYz = yxz — zxy (2.18)
which are to be interpreted as matrix multiplication
тти = мим-мим
The left-hand side involves two vector products [w] = [F][z] and X]w. The right-hand side is the subtraction of the vector M, multiplied by scalar HM from the vector [y], multiplied by scalar MM-
2.2.5.2 Scalar triple product. For any three vectors x, y, and z with X, the skew-symmetric form of x, the scalar triple product, is defined as
V = (xj)z=yXz (2.19)
implying the matrix multiplication
V = [ВДМ = ly][X№
V is the result of the scalar product of two vectors [w] = [Y][y] and [z] and equals the volume contained in the parallelepiped formed by де, у, and z.











