Angular Velocity

As the linear velocity is bom of the displacement vector, so is the angular velocity derived from the rotation tensor by the rotational time derivative. We take a two-track approach. To pay homage to vector mechanics, I present the classical approach to be found in any mechanics text like Goldstein,1 and the general development via the rotational time derivative.

4.2.3.1 Classical Approach. Consider a vector b of constant magnitude rotating about its fixed base point В (see Fig. 4.11). At time t it is displaced from its original position at time Го by

eb = b(t) — b(to)

The time rate of change of eb is the tip velocity v, formed from the limit as At —> 0:

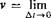b(t) – b(t0) d(sb)

Substitute Eq. (4.25) into this equation:

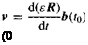
(4.45)

b(0

Because єЬ is small, sR and consequently [d(ef?)/dr] are skew-symmetric tensors (see Sec. 4.1.4). Therefore, Eq. (4.45) presents the vector product of the classical form v = ш x b(t{}) with ш as the angular velocity.

4.2.3.2 General development. Introduce frame A associated with the con­stant b(to) and frame В associated with b(t) (see Fig. 4.12). The two vectors are related by the rotation tensor RBA of the frame В wrt frame A

b(t) = RBAb(t0) (4.46)

To determine the tip velocity of b(t), take the rotational derivative wrt frame A and apply Eq. (4.46) twice:

vA = DAb(t) = DARBAb(t0) = DARBARBAb(t)

We define the angular velocity tensor of frame В wrt frame A as

Пм = DaRbaRba (4.47)

and obtain the tip velocity

Vg = nBAb(t) (4.48)

Comparing Eqs. (4.45) and (4.48) and assuming small displacements 6(r0) ~ b(t), we can relate the time derivative of the perturbation tensor of rotation with the angular velocity tensor

d t

and conclude that because eR is skew symmetric then so is QBA. The angular velocity tensor possesses, therefore, the vector equivalent шВА. For any coordinate system, say ]c, we have the following correspondence:

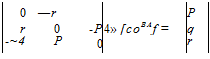(4.50)

Let us solidify the fact that the angular velocity tensor is skew symmetric.

Proof: Show that the angular velocity tensor is skew symmetric.

Start with the null tensor and develop the result:

0 = — E = DA(RBARBA) = DARBARBA + RbaDaRba = ПВА + ПВА at

Therefore, fiBA = —fiBA and ttBA is skew symmetric.

The nomenclature of angular velocity abides by our standards. As indicated, only frames determine its definition, and the superscripts are read from left to right, e. g., fiBA is the angular velocity tensor of frame В wrt frame A. Section 4.2.4 discusses additive properties and other characteristics, which can only be proven after the introduction of the Euler transformation.

Example 4.7 Missile Separating from an Aircraft

Problem. A missile В separates from an aircraft A and descends in the vertical plane. The rotation tensor in aircraft coordinates is given by

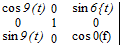
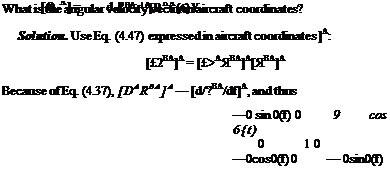A

At cos 0(f) 0 —sin0(f) 0 0 0" X 0 1 0 = 0 0 0 sin0(f) 0 cos 0(f) -0 0 0

and the angular velocity vector is [®BA]A = [0 9 0].

We have added several new concepts to our collection while remaining true to our hypothesis that any phenomena in flight dynamics can be modeled solely by points and frames. Let us review. Displacement Sba uses only points, whereas rotations Rba use only frames. Linear velocities vA} and accelerations aj, mix it up, whereas angular velocities uBA employ only frames. Finally, the rotational time
derivative refers to frames only. Changing its reference frames is the subject of the next section.