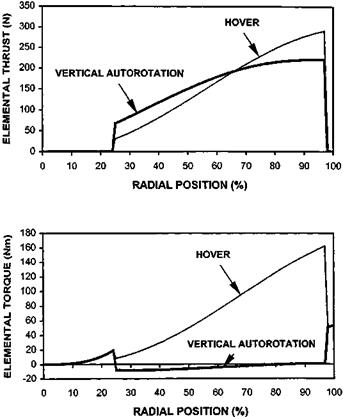
AUTOROTATIVE PERFORMANCE
As a consequence of the problems associated with the vortex-ring state and visually clearing the proposed landing sight, it is common practice for pilots to conduct autorotative descents in forward flight rather than in vertical flight. It is therefore often necessary to determine the performance of helicopters operating in a stable autorotation at some forward airspeed. The approach [2.26] is based on the familiar equations of forward flight and starts by calculating the vertical (FZ) and horizontal (FX) forces that must be balanced by rotor:
FX = 2 pV 2Sf
FZ = mg
where Sf = frontal drag area.
The drag force, FX, gives rise to a power requirement (the parasite power Ppar) which is added to the rotor profile power to give the shaft power (PS) that must be provided by the rate of descent:
PS = Ppr + Ppar = 8 pbcVT RCd(1 + 4.3p2) + FXV
|
Because this shaft power must be extracted from the rotor, by a rate of descent, it is given a negative sign before being normalized using the hover power (PH):
– (P)
where 0 is the disk tilt (tan 0 — FX/FZ) and w0 is the vertical component of the induced velocity.
A momentum analysis of a descending rotor in forward flight yields [2.26]:
(2.27)
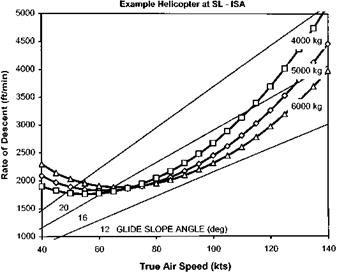
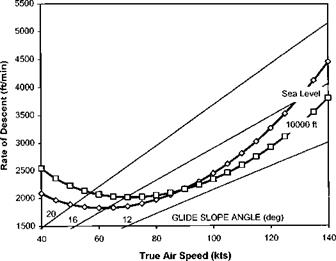
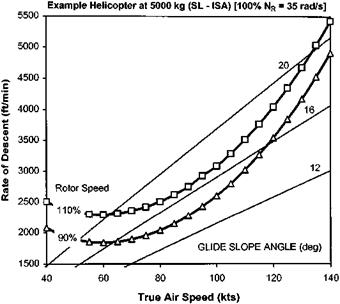
Equations (2.26) and (2.27) can be solved simultaneously for given values of PS/PH, Vf and vih to determine Vv (the autorotative rate of descent, RoD). These equations can also be used to predict the effect of aircraft configuration and flight condition on the autorotative performance, see Figs 2.30 to 2.32, which show the effect of aircraft mass, altitude and rotor speed.
![]()
|
|
|
|
Fig. 2.32 Autorotative performance – effect of rotor speed. |