Our heavyweight helicopter equal in the world does not have
In Rostov started production of the most load-lifting rotary-wing car The Russian holding «Helicopt[...]
Blade element theory
This theory permits direct calculation of the performance of an airscrew and the design of an airscrew to achieve a given performance.
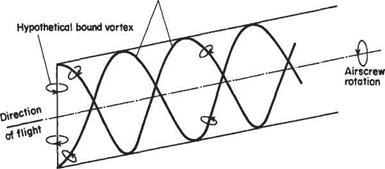
9.4.1 The vortex system of an airscrew
An airscrew blade is a form of lifting aerofoil, and as such may be replaced by a hypothetical bound vortex. In addition, a trailing vortex is shed from the tip of each blade. Since the tip traces out a helix as the airscrew advances and rotates, the trailing vortex will itself be of helical form. A two-bladed airscrew may therefore be considered to be replaced by the vortex system of Fig. 9.8. Photographs have been taken of aircraft taking off in humid air that show very clearly the helical trailing vortices behind the airscrew.
|
Rotational interference The slipstream behind an airscrew is found to be rotating, in the same sense as the blades, about the airscrew axis. This rotation is due in part to the circulation round the blades (the hypothetical bound vortex) and the remainder is induced by the helical trailing vortices. Consider three planes: plane (i) immediately ahead of the airscrew blades; plane (ii), the plane of the airscrew blades; and plane (iii) immediately behind the blades. Ahead of the airscrew, in plane (i) the angular velocity of the flow is zero. Thus in this plane the effects of the bound and trailing vortices exactly cancel each other. In plane (ii) the angular velocity of the flow is due entirely to the trailing vortices, since the bound vortices cannot produce an angular velocity in their own plane. In plane (iii) the angular velocity due to the bound vortices is equal in magnitude and opposite in sense to that in plane (i), and the effects of the trailing and bound vortices are now additive.
Let the angular velocity of the airscrew blades be Г2, the angular velocity of the flow in the plane of the blades be bQ, and the angular velocity induced by the bound vortices in planes ahead of and behind the disc be ±/3f2. This assumes that these planes are equidistant from the airscrew disc. It is also assumed that the distance between these planes is small so that the effect of the trailing vortices at the three planes is practically constant. Then, ahead of the airscrew (plane (i)):
(b – p)£l = 0
i. e.
b = i3
Behind the airscrew (plane (iii)), if u) is the angular velocity of the flow
uj = (b + /3)f2 = 2bfl
Thus the angular velocity of the flow behind the airscrew is twice the angular velocity in the plane of the airscrew. The similarity between this result and that for the axial velocity in the simple momentum theory should be noted.
