Differential equations

The time derivative of the rotation quater­nion is buried in Eq. (4.75), but we have to transform the angular velocity quater­nion first to body coordinates—the body rates are given in body coordinates—and then solve for it. I will spare you the details, although the conversion is not diffi­cult, because the rotation tensor quaternion {QBE}L has its dual in the quaternion transformation matrix {Q}BL related by {QBE)L = [Q}BL. The result is

{QBE}L = -{DBE}B{QBE}L

Partitioning the matrices

and equating the first partitioned columns

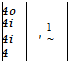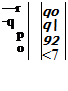we finally obtain, with [соBE]B = [p q r], the desired differential equations

These differential equations are a joy to implement, because they are linear, have no singularities, and number only four. Yet, the initialization with Euler angles is not quite straightforward.

For initialization, we need to express the quaternion components in terms of Euler angles because who wants to describe the launch attitude of a missile in quaternions. Using Eq. (4.71) with Eq. (4.72) to build the three Euler rotations and

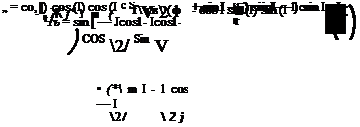combining them q{jt)q(e)q((j>) leads to the relationships

Computational implementation of Eq. (4.77) must maintain the unit norm of the rotation quaternion even in the presence of rounding errors. A proven method is the addition of the factor k).[q to the right-hand side of Eq. (4.77) with к At < {(At integration interval) and к = 1 — (q^ + q + q + <y|) to maintain the unit norm.

The output of the differential equations must be converted to physical meaningful quantities. Those are primarily the Euler angles. Yet, rather than calculating them from the quaternion directly, we take the intermediate steps of rotation tensor and direction cosine matrix to obtain the Euler angles. By this approach we also make available the TM of body wrt local-level coordinates [T]BL.