Effect of Density Altitude

The characteristics of the power required equations make it possible to easily calculate the power required at altitude if the power required at sea level at several gross weights has already been determined. Assuming that the main rotor thrust is equal to the gross weight, the main rotor power equation may be rewritten:

G. W.

P/Po

l,100p 0AVe 1,100

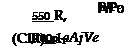and the equation for the tail rotor power in the same form is:

The form of these equations shows that for calculating purposes, weight and density do not have to be treated as separate variables, but that one set of calculations made at sea level at several gross weights can also be used for altitude calculations. For example, Figure 4.38 of Chapter 4 shows the power required by the example helicopter at sea level at several gross weights. To obtain the power required at altitude, the gross weight is divided by the density ratio and the gross weight curve corresponding to this equivalent weight is used. The corresponding values of equivalent power read from the curves are multipled by the density ratio to obtain the actual power.

This method is valid except in those cases where compressibility effects on profile power are significant. Since these effects are a function of temperature

rather than of density ratio, they will have to be estimated separately, by methods discussed in a later section.