Euler Angle Differential Equations

In days past, when computational efficiency was of prime concern, the direct integration of Euler angles was the preferred method. Let us investigate its merit and see why it has fallen from favor. We continue using the Earth as an inertial reference frame and the local-level coordinate system. Starting with the body rates [a>BE]B = [p q r], we develop the differential equations of the three Euler angles ф, в, and ф. A general solution can be derived from Eq. (4.66), but we use a simpler

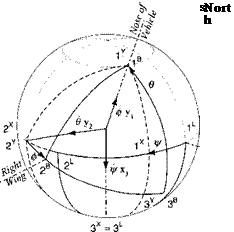derivation based on the property that angular rates can be added vectorially. Figure 4.13 highlights the three Euler rates, which make up the body rates

шВЕ — фх3 + 0y2 + фу і

Selecting body coordinates

[coBE]B = ф[х3]в + Є[у2]в + ф[Уі]в and expressing the base vectors in their preferred coordinate systems

[x3]B = твхшх [y2]B – [T)BY[y2]Y [yif = mBYvyvf

yields the convenient expression of body rates

[a>BE]B = ф[Т]вх[х3]х + [Г]в;r(e[y2lY + <p[yilY)

With the TMs leading up to Eq. (3.14), we can coordinate the body rates

	cos 0	0	—sin 0	"o
[coBE]B =	sinф sin#	COS Ф	sin ф cos 0	0
	cos ф sin 0	—sin ф	COS Ф cos 0	Ф

	‘l 0 o’	(	‘o’
+	0 cos ф sin Ф		в	+
	0 —sin Ф COS Ф		0

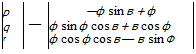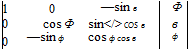Solving for the Euler angular rates yields the desired differential equations:

ф		"і	sin 0 tan 0	cos ф tan в	Р
в	=	0	cos ф	—sin ф	q
ф		0	sin ф / cos в	cos ф / cos в	г

These three nonlinear differential equations, although compact and easily initial­ized, suffer from singularities at vertical climb and dive. Approaching these attitudes, the integration deteriorates and breaks down completely at the singu­larities. Only in older simulations will you still find these equations. They are used by the CADAC FALCON6 simulation. With modem, high-performance computers the old requirement for computational efficiency has given way to accuracy and flexibility. In its train was swept in the ancient quaternion to slove the fundamental kinematic problem. We revive it for the third method.