Flow with Area Change

If the flow is assumed to be isentropic for a channel flow, all states along the channel or stream tube lie on a line of constant entropy and have the same stagnation temperature. The state of zero velocity is called the isentropic stagnation state, and the state with M = 1 is called the critical state.

2.13.4.1 Isentropic Relations

The relations between pressure, temperature, and density for an isentropic process of a perfect gas are:

(2.85)

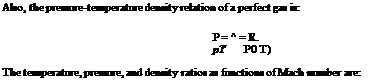(2.86)

(2.87)

where T0, p0 and p0 are the temperature, pressure and density, respectively, at the stagnation state. The particular value of temperature, pressure, and density ratios at the critical state (that is, at the choked location in a flow passage) are found by setting M = 1 in Equations (2.85)-(2.87). For у = 1.4, the following are the temperature, pressure and density ratio at the critical state:

where T*, p* and p* are the temperature, pressure and density, respectively at the critical state.

The critical pressure ratio p*/p0 is of the same order of magnitude for all gases. It varies almost linearly with y from 0.6065, for y = 1, to 0.4867, for y = 1.67.

The dimensionless velocity M* is one of the most useful parameter in gas dynamics. Generally it is defined as:

V V

M* = – = —, (2.91)

a* V*

where a* is the critical speed of sound. This dimensionless velocity can also be expressed in terms of Mach number as: