General rotation

According to a theorem accredited to Euler,1 the general rotation of two frames can be expressed by an angle about a unit rotation vector. We set out to discover this form of the rotation tensor and ask, what are the elements of the rotation tensor in any allowable coordinate system ]й expressed in terms of the angle of rotation ф and the unit vector of the axis of rotation n Iй?

Our itinerary starts with the special rotation tensor [Z?]A of Eq. (4.10) and the special axis of rotation [h]A = [a3]A = [0 0 1], followed by the transformation

to any allowable coordinate system, say Iй, with the TM [ГIй4:

[tf]B = [T]ba[R]a[T]ba

[n]B = [T]BA[n]A

We reach our goal by expressing [і?]й such that it is a function of [nLt and ф only. Let us begin with rewriting [i?]A of Eq. (4.10):

0 0 0

[i?]A = cos ф[ЕА + (1 — cos ф) 0 0 0

0 0 1

‘Yo о

+ sin ф 1 0

0 0

Transforming to [Л]й,

0 0 0

[Я]в = cos ф[Е]в +(1 – cos ф)[Т]ВА 0 0 0 [t]BA

0 0 1

Substituting Eq. (3.4) yields [R]B = cos ф[Е]в + (1 – cos f)[aiB[a^B + sin ir([a2]B[ai]B – [ai]B[a2]B)

(4.П)

Use the coordinates of the base vectors

	a\		1 Q 1___		Гав1 “із
шв =	flB	. шв =	a22	, шв =	а23
			„В		„Я
	_a31_		_аЪ1_		_“зз_

to express the last term bracketed in Eq. (4.11): {[а2ВіаЛВ -Швтв)

О — авав2 + ав2а21 аиаз ~ а\а32 ав ав аПа22 – пв ПВ а2а2 0 а21а32 4” а22а3 -ав2ав{ + “и С1у2 а2аЪ2 а22а3 0 0 —“зз ав 1 а23 азз 0 -“?з ~а23 «13 0

where we used the triad property [я31й = [A |]й[я2]й, with [Ai]B the skew – symmetric form of [ai]B. The last matrix has the skew-symmetric structure of [aUB which is also the unit vector of rotation ГА3]В = [ЛПВ. Replacing in Eq. (4.11) [a3]B, [A3]B by [пв, [ЛПВ yields

[R]B = cos – ф[Ев + (1 — cos ir)[n]B[n]B + sin i(r[N]B

Because ]B is any coordinate system, this equation holds for all allowable coordi­nate systems and, therefore, is the general tensor form of rotations

R = cos j/E + (1 — cos j/)nn + sin j/N (4.12)

So indeed, we confirmed Euler’s theorem that the rotation tensor is completely defined by its angle of rotation xfr and the unit vector of rotation n.

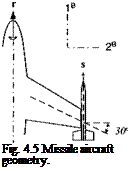
Example 4.2 Boresight Error

Problem. The seeker centerline s of a missile, carried on the right wing tip of an aircraft, is boresighted before takeoff to the aircraft’s radar centerline r (see Fig. 4.5). The antenna unit vector expressed in aircraft coordinates is [rB = [1 0 0]. In flight the wing tip twists upward by 3 deg about the wing box, which is swept back by 30 deg.

1) Calculate the elements of the rotation tensor [RMAB of the missile M wrt the aircraft A in flight.

2) Calculate the components of the seeker centerline in flight [л ]й and give the bore-sight errors in the aircraft pitch and yaw planes in degrees.

Solution. In general, the relationship between the missile and antenna center- line is

s = RMAr (4.13)

1) To calculate [RMA]B, we make use of Eq. (4.12) in body coordinates [Rma]b = cos ir[E]B + (1 – cos ir)[n]B[n]B + sin ir[N]B

With j/ = 3 deg,

[n]B = [-sin 30 deg cos 30 deg 0] = [-0.5 0.866 0]

		0	0	0.866"
+ 0.05234	0	0	0.5
		-0.866	-0.5	0
	0.99897	0.000593	0.045326
	-0.000593	0.99966	0.02617
	-0.045326 –	-0.02617	0.99863

2) To calculate the missile centerline [.? ]11 in flight from the antenna boresight [r]s, we apply Eq. (4.13):

= [RMA]B{r]B =>• [5]B = [0.99897 -0.000593 -0.045326]

The second component is the displacement of the tip of the boresight vector in the 2B direction, which corresponds to an in-turning about the 3s axis (yaw) of —0.000593 rad or—0.034 deg. The third component moves the tip up and is therefore a positive pitch twist of 0.045326 rad or 2.6 deg.

Now we turn to a special rotation tensor with the angle i/r — 90 deg that describes the tetragonal symmetry of missiles.

4.1.2.4 Tetragonal tensor. Missiles with four fins possess tetragonal sym­metry, i. e., their external configuration duplicates after every 90-deg rotation about their symmetry axis. The rotation tensor that models these replications is called the tetragonal tensor Rgo – We derive it directly from Eq. (4.12) by setting xfr = 90 deg:

Rgo = ий + Л^

The tetragonal tensor is composed of the projection tensor P = nh [(see Eq. (2.21)] and the skew-symmetric tensor of the unit rotation vector N. An example should clarify the operation.

Example 4.3 Missile with Fins 90 Deg Apart

Problem. In Fig. 4.6, /| points to the root of fin #1. Use the tetragonal tensor to point to the root of the second fin f2.

Solution. With the base vector b as the unit vector of rotation, we have

f2 = R90fl=bbfr+Bfl (4.14)

The vector/2 is composed of the vector/, projected on b and the component that is the result of the vector product Bfx. With Fig. 4.6 you should be able to visualize this vector addition.

A numerical example can be of further assistance. Introduce the body coordinate system Iй. The vectors^ andf{ have the following coordinates in the body system: [b]B = [1 0 0] and [/, ]c = [/a /12 /13]. The tetragonal tensor becomes

‘1	0	o’		0	0	o’		‘1	0	o’
0	0	0	+	0	0	-1	=	0	0	-1
0	0	0		0	1	0		0	1	0

Fig. 4.6 Tetragonal symmetry.

Applying Eq. (4.14), the second fin has the following coordinates in body axis:

"l	0	o"	fn		fn
0	0	-1	f2	—	-fn
0	1	0	_/l3_		fn

This result is confirmed by Fig. 4.6. The 1 coordinate remains unchanged; the second and third coordinates are exchanged with a sign reversal.