Governing Equations for Flow in General Coordinates

We collect the transport equations for a multi-component, multi-temperature non-equilibrium flow.[178] All transport equations have been discussed in Chap­ter 4, as well as in Chapters 5, 6, 7 (see also [2]—[4]). We write the equations in (conservative) flux-vector formulation, which we have used already for the energy equation in Sub-Section 4.3.2, and for three-dimensional Cartesian coordinates:

of mass and of vibration energy.

The conservation vector Q has the form

Q = [Pi, pu, pv, pw, pet, (A.2)

where pi are the partial densities of the involved species i, Section 2.2, p is the density, u, v, w are the Cartesian components of the velocity vector V, et = є + 1/2 V2 is the mass-specific total energy (V = |V|), Sub-Section 4.3.2, and evibT, m the mass-specific vibration energy of the molecular species m. The convective and the viscous fluxes in the three directions read

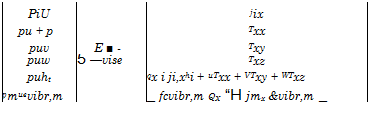(A.3)

(A.4)

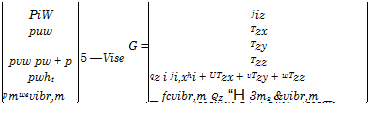(A.5)

The convective flux vectors E_, F_, G represent from top to bottom the transport of mass, Sub-Section 4.3.3, momentum, Sub-Section 4.3.1, of total energy, Sub-Section 4.3.2, and of non-equilibrium vibration energy, Section

5.4. [179] In the above ht = et + р/р is the total enthalpy, eq. (5.7).

In the viscous flux vectors Evisc, F_visc, Gvisc, the symbols jix etc. rep­resent the Cartesian components of the diffusion mass-flux vector j. of the species i, Section 4.3.3, and Txx, Txy etc. the components of the viscous stress tensor r, eqs. (7.10) to (7.15) in Section 7.1.3. In the fifth line each we have the components of the energy-flux vector q, eq. (4.58), Sub-Section 4.3.2, which we have summarized as generalized molecular heat-flux vector in eqs. (4.61) and (4.62), the latter being the equation for the heat flux in the gas at the wall in the presence of slip flow. In the sixth line, finally, we find the terms of molecular transport of the non-equilibrium vibration energy in analogy to the terms of eq. (4.59).

The components of the molecular heat flux vector q in the viscous flux vectors in eqs. (A.3) to (A.4) read, due to the use of a multi-temperature model with m vibration temperatures

The source term S_ finally contains the mass sources Бпц of the species i due to dissociation and recombination, eq. (4.84) in Sub-Section 4.3.3, and the energy sources Qk, m

Qk, m represent the к mechanisms of energy exchange of the m vibration temperatures, for instance between translation and vibration, vibration and vibration, etc., Sub-Section 5.4.

To compute the flow past configurations with general geometries, the above equations are transformed from the physical space x, y, z into the computation space Z, n, C:

Z = Z(x, y,z),

n = n(x, y,z), (A.8)

C = C (x, y,z)-

This transformation, which goes back to H. Viviand [6] and to M. Vinokur [7], regards only the geometry, and not the velocity components. This is in contrast to the approach for the general boundary-layer equations, Sub­Section 7.1.3, where both are transformed. Z usually defines the main-stream direction, n the lateral direction, and C the wall-normal direction, however in general not in the sense of locally monoclinic coordinates, Sub-Section 7.1.3. The transformation results in

dQ дЩ + Ш-visc) _|_ + Eyjsc) 9(G + Gvisc) = g (A 9)

dt dZ di] dQ ~’

which is the same as the original formulation, eq. (A.1).

The transformed conservation vector, the convective flux vectors, and the source term are now

U = J~lU,

E=J-%,E+ZyF + Z, Gl F = J-l[ilxE + ilvF + ilzG], (A.10)

G = J-1[C, E + CyF + CM,

S = J-ls,

with Jbeing the Jacobi determinant of the transformation. The trans­formed viscous flux vectors have the same form as the transformed convective flux vectors.

The fluxes, eqs. (A.3) to (A.5), are transformed analogously, however we do not give the details, and refer instead to, for instance, [8, 9].