Kinematics of Changing Times

We are now prepared to invite time into our Euclidean three-dimensional world and develop the tools to study the kinematics of motions. Motions are modeled by including time dependency in the displacement vector and the rotation tensor. Hence, if sBa is the displacement vector of point В wrt point A, Sba(0 describes the motion of point В wrt reference point A. Likewise, RBA(t) models the changing orientation of frame В wrt the reference frame A.

Other kinematic concepts are formed by the time rate of change of displacement and rotation. Linear velocity is the first and acceleration the second time derivative of displacement. Angular velocity is obtained by the time derivative of rotation. For instance, the linear velocity of point В wrt frame A is produced by vAH = (d/dt)«AB – Yet these new entities require close scrutiny if we want them to be tensors. Remember, physical models, like velocity, maintain their tensor property only if their structure remains invariant under coordinate transformations. As long as the coordinate transformations are time invariant, the time derivative does not change the tensor characteristic of its operand, but our modeling strategy is more ambitious. We require that the time derivatives of tensors are tensors in themselves, even under time-dependent coordinate transformations.

Pick up any textbook on mechanics and you find the following treatment of the time derivative of vector s transformed from A to В coordinate system:

where ш is the angular velocity between В and A. Unfortunately, the right side has an additional term, and thus the time derivative destroyed the tensor property of the derivative of vector s.

Let us translate Eq. (4.34) into our nomenclature. With any two allowable co­ordinate systems J’4 and ]B the vector s transforms like a first-order tensor:

[S]A =

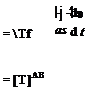Taking the time derivative and applying the chain rule

and exchanging the sequence of transformation in the last term by transposition yields

Comparison with Eq. (4.34) shows that the right and left sides are related by the TM [T]AB and that the ш vector corresponds to the term |T |/M [dT/dt]B’4.

From Eq. (4.35) it is clear that the time derivative of s does not transform like a first-order tensor. If, however, we could define a time operator that would give the right and left side the same form, the tensor property would be maintained. Does such an operator exist? Indeed it does, and it is called the rotational time derivative.

Back in 1968, pursuing my doctoral dissertation, I found in Wrede’s book2 on vector and tensor analysis just the concept I needed. He defines a rotational time derivative, whose operation on tensors preserves their tensor property. It is couched in hard-to-understand tensor lingo; but applied to right-handed Cartesian coordinate systems, the concept is easy to grasp. Later I discovered that Wrede’s work was preceded by Wundheiler’s (Warsaw, Poland) research, in 1932.3