Launching a spacecraft

A projectile, whether it is launched for the purpose of escaping from the earth, or landing on the moon, or becoming a satellite, or simply travelling over the earth’s surface to some other place, must first pass through the atmosphere.

Fig 13B Lift off for the moon

(By courtesy of the General Dynamics Corporation, USA)

The most important effect of this is that we cannot neglect air resistance, as we have so calmly done throughout this chapter (though with constant reminders). And the practical effect of air resistance is to reduce speeds, so the actual speeds of launching within the atmosphere must all be higher than those we have given. How much higher? From ground level, something of the order of 10 or 12 per cent, e. g. if the escape velocity is 40 250 km/h (11.134 km/s), the actual velocity of launch at ground level would have to be about 45 000 km/h (12.5 km/s), and for a circular velocity of 29 000 km/h (8.05 km/s), say 32 000 km/h (8.9 km/s). This naturally makes accuracy more difficult to achieve.

But there is a further difficulty. The launching speed cannot be attained at ground level. As has already been explained, the body on the first part of its flight is propelled by rockets; if it is required to reach great heights by multi­stage rockets. So in contrast with a shell fired from a gun there is time – and distance – in which to gather speed; and by so deciding and regulating the thrust of the rockets in relation to the mass of the projectile, and taking into account the drag due to air resistance, the acceleration can be moderated suf­ficiently to prevent damage to the missile itself and its mechanisms, and if passengers are to be carried, even to human beings. This moderation of the acceleration is of course an advantage, but it also makes it extremely difficult to calculate just what the speed, direction, and height of the vehicle will be when it is finally launched, i. e. when the fuel of the last launching rocket has been exhausted.

No one who has thought of this problem, even in the very elementary form such as we have attempted to explain in this book, can be anything but amazed at the accuracy that has actually been achieved in the launching of spacecraft.

As greater heights are reached there is less density of air, and so the drag decreases in spite of ever-increasing speeds. Eventually the rocket power is shut off, the last stage of the launching rocket is jettisoned, and the projectile, or spacecraft, or whatever it may be, travels on its elliptical path under the force of gravity until it begins to descend and again approaches the earth’s atmos­phere. The distance it travels during this ballistic phase – under its own steam, one might almost say! – will depend on the velocity it had achieved and the direction in which it was travelling when the rocket power ended. It may be hundreds or thousands of kilometres, it could be round the earth and back again, or several times round; there is no fundamental difference between a missile, a satellite and a spacecraft, they differ only in the speed, direction and height of launch.

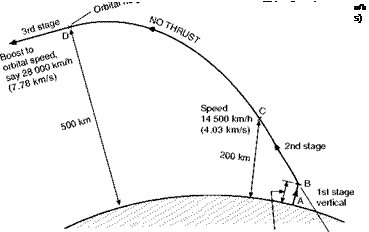
The fact that the final launch takes place at considerable height does, at least, provide partial justification for our earlier neglect of air resistance when considering their motion. It is true that in thinking of launches at a height of 800 km we may have been guilty of going rather far though, as explained at the time, it had the advantage that we really could neglect air resistance, and so the speeds we gave for that height were reasonably correct. Typical figures for an actual launch (Fig. 13.13, overleaf) are to a height of 60 km and a speed of 6000 km/h (1.67km/s) at the end of the first stage, 200 km and 14 500 km/h (4.03 km/s) at the end of the second stage, and 500 km and 28 000 km/h (7.78 km/s) at the end of the third stage. The take-off is vertical, the path is then inclined at say 45°, then when the velocity is sufficient there is a period of coasting or free-wheeling between the second and third stages to the required height (which will become the perigee if the missile is to be a satellite) where the path will be horizontal, then the third stage rocket boosts the velocity to that required for orbit. The more this exceeds the circular velocity, the more distant will be the apogee. The perigee of nearly all the early satellites was less

than 800 km, but the apogee varied from just over 800 km for Sputnik 1 up to – well, to the moon and beyond.

The second stage, orbiting the earth, has already been considered in some detail, and there is little to add. This is the aspect of space flight of which we have had most experience, and there are now literally hundreds of ‘bodies’ of various shapes and sizes and masses orbiting the earth, and on a variety of orbits, and hundreds more that have finished their flights and have been burnt up on re­entering the atmosphere. There have also been several manned orbits of the earth, and space stations have been set up which can be permanently manned in ‘shifts’ by shuttle services, put together and enlarged up there, and used for a variety of purposes, some peaceful – others perhaps not so peaceful.

So far as going to the moon is concerned the first orbits are more or less cir­cular and then, at the third stage, at exactly the correct part of the orbit, a burst of power is given to boost the speed and put the spacecraft on its journey to the moon. Although this journey is often represented in diagrams as a straight line it is in fact merely an elongated elliptical orbit designed to pass near the moon, so the astronauts still experience the sensation of ‘weightless­ness’. Mid-course and other corrections, if required, can be given by short bursts of rocket power; since there is no air resistance the thrust required to make such changes is not very great. As in all elliptical orbits the speed will decrease as the apogee is approached, but by then the spacecraft will have passed the neutral point, will be attracted by the moon and will again pick up speed, but now new problems arise and we must consider how orbits of the moon differ from those round the earth.

Fig 13.13 Typical flight path for launching of spacecraft Not to scale.