Linear Momentum

Have you experienced your linear momentum lately? Probably not if it remained constant. As an Earthling of 80 kg mass, you were bom with a linear momentum wrt the ecliptic of about 2.66 x 106 kg m/s and because the sun is part of the Milky Way galaxy, you can claim another 4.4 x 1010 kg m/s of linear momentum. That much should make anybody dizzy, but nobody takes notice. If, however, you travel in a car at 60 miles/h and hit a wall, your 2100 kg m/s change of linear momentum will kill you. It is the time rate of change of linear momentum that creates the force; Newton just reversed the order of cause and effect.

Before we apply Newton’s law, we need to learn more about the linear momen­tum. First we define the linear momentum of a particle, then generalize it for a collection of particles (body) and single out its c. m. For clusters of bodies, we learn how to calculate their linear momentum, again with special emphasis on the common c. m.

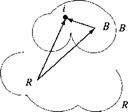
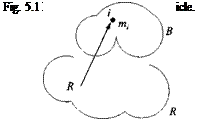
Definition: The linear momentum pf of a particle і relative to the reference frame R is defined by the rotational time derivative wrt to frame R of the displace­ment vector siR multiplied by its mass иг,- (see Fig. 5.1).

pf = mjDRSiR = ttiivf (5.1)

Because the rotational derivative of the displacement vector yields the velocity

vf = DRSjK, we can also state

linear momentum = mass x linear velocity

The linear velocity vector imparts the direction to the linear momentum and also its independence from a specific reference point. The nomenclature reflects that char­acteristic: subscript і is the particle point and superscript R an arbitrary reference frame.

Definition: The linear momentum of a collection of particles В relative to the

reference frame R is the sum over all linear momenta of each particle

(5.2)

This definition is awkward because it requires knowledge of every particle’s ve­locity. We can simplify matters greatly, by defining the c. m. В of the collection of particles В with total mass mB and specifying its velocity vR. Then, the linear momentum pR of c. m. В wrt the reference frame R is given by

Only the total mass and the c. m. of body В contribute to the linear momentum. The shape and attitude of the body are irrelevant. In effect, Eq. (5.3), in the light of Eq. (5.1), can be interpreted as the linear momentum of a particle with mass mB and linear velocity of point B. One only should add that В has to be the c. m. The simplicity of the notation emphasizes this fact. Let us prove Eq. (5.3) by Eq. (5.2).

Proof: From Fig. 5.2 we deduce the displacement vector triangle

siR — S ІВ + SBR

Take the rotational derivative wrt the reference frame

DRsiR = DRsiB + Drsbr

Substitute it into the second term of Eq. (5.2), and, because the mass of each particle is constant, it can be brought inside the rotational derivative

‘Y^miDRsiR = ‘Y^miDRsiB + ‘^2miDRsBR =

Fig. 5.2 Linear momentum of body B.

The next to the last term is zero because, if В is the common c. m., then JT т^ів — 0, and the rotational derivative of a null vector is zero. Therefore,

Y^miDRsiR = mBvl

І

The collection of particles, forming body B, does not have to be mutually fixed. As long as their c. m. and total mass are known, the linear momentum can be calculated.

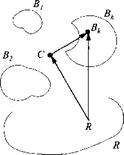
We can extend the computation to a collection of bodies B^, к = 1, 2, 3 … as shown in Fig. 5.3. Because bodies can be regarded as particles as long as their individual c. m. are used as representative points, we can use Eq. (5.2) to sum their individual contributions and calculate the total linear momentum:

PRBk = Y^Pb, = Y^rnBkDRsBkR (5.4)

к к

Introducing the vector triangle for each body, with C the common c. m., and taking the rotational time derivative wrt the reference frame R

DRsekR — DRSBkc + DRScr

yields

РІвк = ^mBtDRSBkC + ^mBtDRsCR

к к

Because C is the common c. m., the first term vanishes as long as the mass of each

body remains unchanged:

^т8‘ЛВіС = /)й|^тйіС| =£>*0 = 0

Therefore, the linear momentum wrt a reference frame R of a collection of bodies £/£. к = 1, 2, 3,…, not necessarily rigid but with constant mass, is calculated from the total mass m^ mBl and the linear velocity v* of the common center of mass wrt the reference frame

РІвк = = m^vRc (5.5)

к

We have two methods to calculate the linear momentum of clustered bodies. If we know the individual values, we just add them together [see Eq. (5.4)], or we use Eq. (5.5) if the cluster properties are known.

Example 5.1 Linear Momentum of Reentry Bodies

Problem. A ballistic missile with 3000 kg of payload descends at 12,000 m/s and releases three nuclear warheads at 800 kg each and deploys six 100-kg decoys. Use two ways to calculate the linear momentum of the cluster of reentry bodies.

Solution. Using individual bodies, the total linear momentum is P*Bk=Yl, PBk = YlmBlvBt=( 3x 800 + 6 x 100) x 12,000 = 36 x 106kgm/s

к к

or using the cluster

p%Bk = = 3,000 x 12,000 = 36 x 106kgm/s

both methods lead to the same result.

The linear momentum is an essential ingredient of Newton’s second law. As we add forces to the thought process, the kinematic world view becomes dynamic, and we can study the interactions of force, velocity, and mass in time.