Linear Velocity and Acceleration

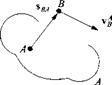
At several occasions we have encountered already the linear velocity v j) of point В wrt frame A. Now we have to assign it a definition (refer to Fig. 4.9). Given

Fig. 4.9 Linear velocity.

is the frame A and the displacement vector sBA, where В is any point and A is a point of frame A. The linear velocity of point В wrt frame A is obtained from the rotational time derivative wrt frame A, applied to the displacement vector sBA:

vAB = Dasba (4.40)

The notation of the linear velocity vector does not carry over the identity of point A, but just refers to the frame A. This simplification is justified by the fact that any point of frame A can serve as reference point.

Proof: Show that the point A in Eq. (4.40) can be any point of frame A. Let A1 and A2 be any two points of frame A. Then sBA = sBA2 + sA2A. Take the rotational time derivative on both sides and use the second part of Property 1:

DASba 1 — DASBA 2 + DASA2Al

However, DasA2A — 0 because the displacement vector s,2a i is fixed in frame A. Therefore,

Dasba 1 = Dasba2 – vB

The fact that DasA2Ai = 0 can be verified from Eq. (4.36). Pick ]A as a coordinate system associated with frame A. Then

dSA2Al	A	[dTl
d t	+ [T]	_ ^ _

_DASA 2Ai]

[Sa2Ai]a.

Both terms are zero. The first term is an ordinary time derivative of a vector with constant length, and the second term takes the time derivative of a unit matrix. If a tensor is zero in one coordinate system, it is zero in all coordinate systems.

Example 4.6 Differential Velocity

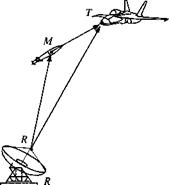
Problem. A missile with c. m. M is attacking a target, point T (see Fig. 4.10). Both are tracked by the point antenna R of the radar frame R. What is the velocity of the target wrt the missile as observed from the radar?

Solution. The displacement vector of the target wrt to the missile is

Fig. 4.10 Differential velocity.

We take the rotational derivative wrt the radar frame R and apply the linear operator property

DrStm = Dr(str — sMr) — DrStr — DrsMr

According to the linear velocity definition Eq. (4.40), the right-hand sides are DrStr — and DrSmr = vRM. The term on the left however is different. None of its points belongs to the radar frame. Rather the two points relate the target to the missile. Its rotational derivative wrt to the radar frame forms the desired velocity. We name it the differential velocity of T wrt M as observed from frame R and write

(4.42)

The concept of differential velocity is particularly important in missile engage­ments and will surface again in our discussion of proportional navigation.

In this example we encounter two types of linear velocities distinguishable by their reference points. If the reference point is part of the reference frame, we speak of the relative velocity, or just velocity (e. g., vR) otherwise, if the reference point is not part of the reference frame, we refer to it as differential velocity (e. g., vRM).

The linear acceleration aAB of a point В wrt the reference frame A is defined as the second rotational derivative of the displacement vector sBA, or the first derivative of the velocity vector

If the reference point A is part of the reference frame A, any point of that frame can be used, and thus the nomenclature aB does not explicitly identify the reference point A. (It may be beneficial at this point to remind you that without exception points are subscripts and frames are superscripts.) This type of acceleration, relative to reference frame A, is also called relative acceleration to distinguish it from the differential acceleration.

Referring to Fig. 4.10, the concept of differential acceleration is similar to differential velocity. If we take the second rotational derivative of the displacement

vector Eq. (4.41), we obtain

DrDrStm = DrDrStr — DrDrsMr

On the right-hand side the reference point R is part of the reference frame R, and therefore the two terms are the relative accelerations DrDrSjr — aR and DR DRsMR=allt. The term on the left contains the reference points T and M that do not belong to frame R. Hence, we are dealing with the differential acceleration Dr DrStm = ar. M’ which is the difference of the two relative accelerations

атм — ат ам

Linear velocities and accelerations are important building blocks in any simula­tions. You will have ample opportunity to use them as modeling tools of aerospace vehicles. Yet our toolbox is incomplete without the angular velocities and accel­erations.