Quaternion Differential Equations

Would you believe that the introduction of quaternions preceded vectors and tensors? Sir W. R. Hamilton published in 1843 his quaternion algebra,5 which contained, albeit hidden, three-dimensional vectors.

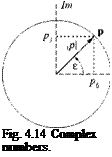
Quaternions are vectors in four-dimensional space, therefore their distinctive name. A simpler version, complex vectors, are their cousins in two dimensions. In Fig. 4.14 we consider the number 1 on the real axis as the first base vector and, on the imaginary axis, і as the second base vector. The two-dimensional vectorp can be expressed in the component form/? = l/?o + i/?i – With the angle of rotation e and absolute value | p known, we can also represent the complex variable in the polar form/? = реіє.

Now let us transition to four-dimensional space. We already encountered in Sec. 4.1.1 Euler’s theorem of rotation, which states that four parameters specify an arbitrary rigid rotation. There are three components for the axis of rotation n in addition to the angle of rotation e (see Fig. 4.15). Quaternions with unit norm represent such rotations in four-parameter space. Hamilton generalized the

1

two-dimensional complex number space by adding two more imaginary axes j and k. Embedded in this four-dimensional space is the rotation quaternion in the component form

q = qo+iqi + jqi + kq3 (4.71)

where ij = k, jk = i, ki = j and i2 = j2 = k2 — — 1 and its norm q% + q2 + q2 + q = 1.

Hamilton created a complete quaternion algebra with vectors as a special case. It is therefore not surprising that many concepts, which we have introduced in three- space, have their counterparts in four-space. To develop the quaternion differential equations, I shall make use of several entities. The rotation quaternion {q}, just introduced, the rotation tensor quaternion of frame В wrt frame E {QBE}, and the angular velocity quaternion of frame В wrt frame E The use of braces

identifies them as tensors in four-dimensional space, which, when coordinated, receive a superscript for the coordinate system.