. Rotation quaternion

The rotation quaternion has four coordinates q0, qi, q2, and q3 with direct relationship to the four Euler parameters n and є. In any coordinate system, with braces designating four-dimensional and brackets three-dimensional Euclidean space

This relationship gives us a vivid picture of a rotation quaternion. The scalar component qo = cos(e/2) contains the half-angle of rotation, and the vector part

relates to the unit vector of rotation [и]. The mystery of four-dimensional space is explained if we consider the rotation quaternion consisting of a scalar part qo and

2L

Fig. 4.16 Yaw rotation.

a three-dimensional vector [q

A simple example may help your intuition.

Example 4.11 Rotation Quaternion

Problem. Body frame В is rotated wrt Earth frame E by the angle ф = 60 deg about the vector of rotation [n]L = [0 0 1] in local-level coordinates (see Fig. 4.16). Calculate the rotation quaternion {qBE}L.

Solution. Introducing local-level coordinates into Eq. (4.73) and with Eq. (4.72) provides

cos(i/r/2)

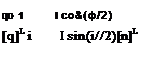
sin(^/2)n!

sin(^/2)«2

sin(^/2)n3

Using the rotation vector and the numerical values of the example yields the rotation quaternion

cos(i/f/2)		0.5V3′
0	_	0
0		0
sin(i/f/2)«3		0.5

This is the rotation quaternion of the first Euler rotation about the angle yaw. The other two rotations about pitch and roll follow similar patterns.

4.3.3.2 Rotation tensor quaternion. As a vector has a skew-symmetric tensor equivalent, so does the rotation quaternion have a tensor equivalent. It

consists of the scalar part multiplied by the unit tensor quaternion and an additive skew-symmetric tensor quaternion

(4.75)

Compare this definition with that of the three-dimensional space

The factor two of the quaternion definition grabs your attention, but is understand­able because quaternions operate with half angle of rotation. Because Eq. (4.75) involves rotation tensor quaternions, the angular velocity quaternion is also a tensor quaternion, yet without a scalar part

Not surprising, the vector part is the angular velocity vector of three-space.

We have assembled all required elements to proceed with the quaternial solution of the fundamental kinematic problem in flight simulations. Rearranging Eq. (4.75) will deliver the differential equations.