Rotation Tensor Differential Equations

The first approach is based on the definition of the angular velocity tensor, Eq. (4.47) referenced to body frame B. If expressed in body coordinates, the rotational derivative reduces to the ordinary time derivative [see Eq. (4.37)]:

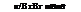
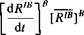[£2,B]B = [£>вЯ7в]в[Я/в]

Solving for the time derivative

[dRIB~

d t

produces the differential equations for the nine elements of the rotation tensor.

In simulations, rather than calculating the rotation tensor, the focus is on the TM of body wrt inertial coordinates. The connection is provided by Eq. (4.6), | T]111 = [RBI]B, which we can apply directly to Eq. (4.64):

bi _____

= (4.66)

These are the famous differential equations of the direction cosine matrix. You will see them again in Sec. 10.1.2 when we formulate the six-DoF equations of motion over an elliptical Earth. In simpler simulations, when Earth E serves as an inertial frame, the local-level system is used. Therefore, we replace frame / by E:

bl _____

= [£2№]В[Г]“- (4.67)

where [T]BL relates to the Euler angles of Eq. (3.28). If the Euler angles are given at launch, use Eq. (3.28 ) to initialize the nine elements.

The nine differential equations are not independent. Because the TM is com­posed of three orthonormal base vectors, only six differential equations need be solved, and the remaining three elements can be calculated from the orthogonal­ity conditions. Express the direction cosine matrix in the three base vectors of the geographic frame [T]BG = [[gj]B [#2ІЙ and substitute them into the

differential equation, Eq. (4.67),

£[[ЫВ Шв Ыв] = [^]*[[gi]B шв ыв]

Take the first two columns individually, add an orthogonality condition, and you have the set of six differential and three algebraic equations:

^[gi]B = [^]B[g!]B

ck

^[g2]B = [^]B[g2]B (4.68)

ck

Шв = [Gi]B[g2]B

To recover the Euler angles, use Eqs. (3.15-3.17) or an alternate form that is used in flight simulators:

(4.69)

where the tij are the elements of the direction cosine matrix. Equation (4.69) de­livers similar results as Eqs. (3.15-3.17). The sign function—FORTRAN intrinsic function SIGN(A, B)—controls the sign like the FORTRAN ATAN2(A, B) function in Eqs. (3.15-3.17). The range of the angles is — ж < ф < +n, —ж < ф < +ж, and —ж/2 < в < +ж/2.

With these types of Euler angles adopted for flight mechanics, singularities oc­cur at в = ±jt/2, where no distinction is possible between yaw and roll. These correspond to a vertical dive or climb, situations seldom encountered in airplanes, but important in missile launches. Resequencing the Euler angles can place the singularity at another less conspicuous attitude. Fortunately, this undesirable be­havior occurs only in the output calculations and not in the differential equations themselves, where they would provoke much more trouble.

Integrating the differential equations on digital computers with finite word length and incremental time steps produces errors that corrupt the TM. To maintain or­thogonality, a correction term is applied from integration step n to n – f – 1:

[T(n + l)]s/ = [Т(п)]ш + ([E] – [T(n)]BI[T(n)]B!)[T(n)]BI

As a sanity check, note that the correction term is zero for orthogonal TMs. For details however you have to wait until Sec. 10.1.2, which describes the implemen­tation as part of a six-DoF simulation. The actual code can be found in the CADAC GHAME6 simulation.

The rotation tensor and direction cosine matrix solutions have superior features that lend themselves to computer applications. The differential equations are linear, well behaved, and without singularities. Above all, the important direction cosine matrix is directly computed. However, because Euler angles are so much easier to visualize, initialization and output have to be converted. To avoid this conversion, the Euler angles can be integrated directly.