Small Rotations

Isn’t it interesting that the orientation between two frames, although determined by unit vector and angle, requires a second-order rotation tensor for portrayal? If several rotations are combined, the sequence is not arbitrary because the multipli­cation of second-order tensors does not commute. Both attributes are simplified, however, if we deal with so-called small rotations. Small rotations reduce to vectors and can be combined in any order.

Engineers like to deal with small quantities. They are so much easier to model because the mathematics is simpler. Consider the stability equations of aircraft with their implicit small angle assumption and the error equations of INS systems. These small perturbations simplify the analysis, resulting in linear differential equations, the darlings of engineering analysis.

єЬ

b(t0)

er

Fig. 4.8 Small rotation.

I will guide you from the general rotation tensor to the perturbation tensor of rotation, the small rotation vector, and finally, the small rotation tensor. All of these concepts are important and should be in your toolbox. We will start with the question: what is the form of the rotation tensor if a vector is rotated by an infinitesimal small amount?

Rotate vector b from its initial position b(to) through rotation tensor R to its current position

b(t) = Rb(t0) (4.22)

The difference eb between the two vectors is, as shown in Fig. 4.8, sb = b(t)—b(t0) and with Eq. (4.22)

	eb = (R — E)b(to)	(4-23)
Introducing the definition of the perturbation tensor of rotation
	eR = R – E	(4.24)
into Eq. (4.23) yields	eb = eRb(t0)	(4.25)

The displacement vector eb is the result of the multiplication of a tensor eR with the initial vector. What is the property of this tensor?

Because R is orthogonal, RR = E, and from Eq. (4.24)

E = (eR + E)(eR + E) = E + eR + eR + eReR

Now we assume that є indicates a small quantity. Then the last term is small to the second-order wrt the other terms and can be neglected. Thus eR = —eR, i. e., the perturbation tensor eR is skew-symmetric and thus can be represented by a vector. For any allowable coordinate system |-4 the perturbation tensor has the components

ern	ЄГ12	er 13
ЄГ21	ЄГ22	ЄГ23
ЄГ31	ЄГ32	ЄГ33

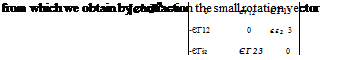but if it is skew-symmetric it has only three independent components,

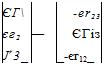(4.27)

Finally, the tensor R for small rotations consists according to Eq. (4.24) of the unit tensor and the perturbation tensor Eq. (4.26). Expressed in any allowable coordinate system A, it becomes

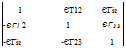(4.28)

By now you may be thoroughly perturbed by all of these perturbations. Let us recap. The rotation tensor of a small rotation between two frames, say В wrt A, Rba, consists of the unit tensor E and the perturbation tensor of rotation sRBA

RBA = E + sRba

where sRba can be reduced to a small rotation vector er. To clarify these concepts, let us look at an example.

Example 4.5 INS Tilt

An INS maintains a level reference either by a gimbaled platform or a computed reference frame. Yet, mechanical or computational imperfections cause the refer­ence to deviate from the true values. These errors, called tilts, are rather small and are measured in arc seconds.

The tilt angle в (pitch) of an INS platform about the east direction gives rise to the rotation tensor expressed in geographic axes ]G

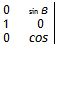
[Rtf)]0 =

Because the tilt is a very small angle єв, we introduce the small angle assumption

(4.29)

with the corresponding small rotation vector [ег(єв)]в = [0 єв 0]. Similar small rotation tensors can be developed for the tilt ф about the north direction and the azimuth error ф:

	‘l	0	0		‘ 1	—еф	0
[tf(e0)]G =	0	1	—еф	; тєф)]° =	еф	1	0
	0	еф	1		0	0	1

The complete tilt tensor consists of the product

[Я(еф, ев, еф)]с = [Я(є0)]с[Л(є0)]о[Я(еіА)]с

and the multiplications carried out

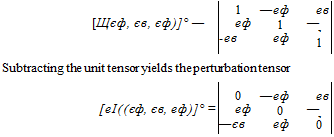(4.31)

(4.32) from which we obtain by analogy with Eqs. (4.26) and (4.27) the small rotation vector

[єг{еф, ев, еф)]° = [еф єв еф] (4.33)

Here you experienced all three notions: small rotation tensor, perturbation tensor of rotation, and small rotation vector. You can convince yourself of the commu­tative property of small rotations by changing the sequence of multiplication in Eq. (4.30) and each time arriving at the same result Eq. (4.31)

This insight into perturbations prepares you to follow the derivation of an INS error model in Sec. 10.2.4, which is used in six-DoF simulations. The tilt tensor, with its tilt vector, models three of the nine INS error states. Another application of importance is the derivation of the perturbation equations of air vehicles, Sec. 7.2. You will find again a small rotation tensor describing the deviation of the perturbed flight from the reference flight.

We have about exhausted the topic of rotation tensors. As the displacement vector models the location of point В wrt point A, so does the rotation tensor establish the orientation of frame В wrt frame A. Both together define the position of frame В wrt frame A (refer to Sec. 3.1.1). We established the tensor characteristic of rotations and the special circumstances under which they relate to transformation matrices. You should by now be convinced that both are different entities! We dealt with special rotations like the tetragonal symmetry tensor and small rotations. A correct understanding of these concepts will make it easier for you to grasp the following kinematic developments.