The performance of a blade element
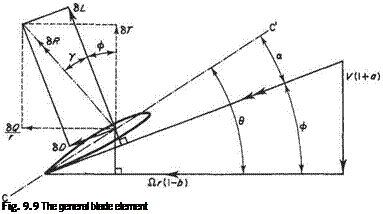
Consider an element, of length 6r and chord c, at radius r of an airscrew blade. This element has a speed in the plane of rotation of Qr. The flow is itself rotating in the same plane and sense at Ш, and thus the speed of the element relative to the air in
this plane is flr(l — b). If the airscrew is advancing at a speed of F the velocity through the disc is F(1 + a), a being the inflow at the radius r. Note that in this theory it is not necessary for a and b to be constant over the disc. Then the total velocity of the flow relative to the blade is Fr as shown in Fig. 9.9.
If the line CC’ represents the zero-lift line of the blade section then в is, by definition, the geometric helix angle of the element, related to the geometric pitch, and a is the absolute angle of incidence of the section. The element will therefore experience lift and drag forces, respectively perpendicular and parallel to the relative velocity Fr, appropriate to the absolute incidence a. The values of Cl and Co will be those for a two-dimensional aerofoil of the appropriate section at absolute incidence a, since three-dimensional effects have been allowed for in the rotational interference term, MI. This lift and drag may be resolved into components of thrust and ‘torque-force’ as in Fig. 9.9. Here SL is the lift and 6D is the drag on the element. <57? is the resultant aerodynamic force, making the angle 7 with the lift vector. 6R is resolved into components of thrust 6T and torque force SQ/r, where SQ is the torque required to rotate the element about the airscrew axis. Then
|
tan7 = SD/SL = CD/CL |
(9.24) |
|
Fr = F(1 + a)cosec </> = flr(l — Ь)ъесф |
(9.25) |
|
ST = <57?cos(</> + 7) |
(9.26) |
|
Щ – = SRsin(<j) + 7) |
(9.27) |
|
t ^ F(1 + a) •“* = Пг(1-4) |
(9.28) |
The efficiency of the element, 771, is the ratio, useful power out/power input, i. e.
![]() VST V cos (<ft + 7)
VST V cos (<ft + 7)
^1 Si SQ Sir sin(</> + 7)
 |
Now from the triangle of velocities, and Eqn (9.28):
whence, by Eqn (9.29):
|
|
|
|
|
|
 |
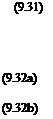 |
Let the solidity of the annulus, <7, be defined as the ratio of the total area of blade in annulus to the total area of annulus. Then
From Fig. 9.9
ST = SL cos ф – SD sin ф
— BcSr^pV{CLcosф – C£isin^)
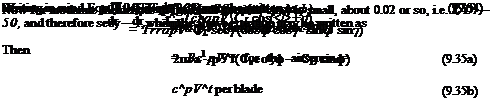 |
Therefore
whence, using Eqn (9.32a and b)
= 2nr2a^pV^(C£ sin^ + Co cos ф)
|
Writing now
is equal to the product of the rate of mass flow through the element with the change in the axial velocity, i. e. ST = mSV. Now |
m = area of annulus x velocity through annulus x density = (27rr<5r)[F(l + a)p = livrpSr V(l + a)
AV = Vs – V = V(1 + 2a) – V = 2aV
whence
ST = 2TrrpSrV22a(l + a)
giving
![]()
|
|
|
|
|
|
|
|
In the same way, by considering the angular momentum
SQ = mAwr1
where Aw is the change in angular velocity of the air on passing through the airscrew. Then
![]() SQ = (2irr8r)pV{ + a)(2bQ)r2
SQ = (2irr8r)pV{ + a)(2bQ)r2
= 47rr3pF6(l + a)Q6r
![]()
^ = 4nr3pVb(l + a)Q,8
Now, as derived previously,
^ = 7ГPvqpVl (Eqn (9.37a))
Substituting for FR both expressions of Eqn (9.25), this becomes = m^trplVfi + fl)cosec0][I2r(l — b) sec^
Equating this expression for dQ/dr to that of Eqn (9.41) gives after manipulation
61 / ,
——— = – crq cosec ф sec ф
1 — b 4
![]() = ^aq cosec 2ф
= ^aq cosec 2ф
The local efficiency of the blade at the element, r? i, is found as follows.
(SlT
Useful power output = V ST = F—<5r
Power input – 2xn SQ 2-717? Sr
Therefore
F dT/dr ^ 27Г7І dQ/dr
V 2жra pVt 2жп 2тггга jpV^q
V ![]() t 2mr q
t 2mr q
which is an alternative expression to Eqn (9.30).
With the expressions given above, dT/dr and dQ/dr may be evaluated at several radii of an airscrew blade given the blade geometry and section characteristics, the forward and rotational speeds, and the air density. Then, by plotting dT/dr and
dQjdr against the radius r and measuring the areas under the curves, the total thrust and torque per blade and for the whole airscrew may be estimated. In the design of a blade this is the usual first step. With the thrust and torque gradings known, the deflection and twist of the blade under load can be calculated. This furnishes new values of 9 along the blade, and the process is repeated with these new values of 9. The iteration may be repeated until the desired accuracy is attained.
A further point to be noted is that portions of the blade towards the tip may attain appreciable Mach numbers, large enough for the effects of compressibility to become important. The principal effect of compressibility in this connection is its effect on the lift-curve slope of the aerofoil section. Provided the Mach number of the relative flow does not exceed about 0.75, the effect on the lift-curve slope may be approximated by the Prandtl-Glauert correction (see Section 6.8.2). This correction states that, if the lift curve slope at zero Mach number, i. e. in incompressible flow, is ao the lift-curve slope at a subsonic Mach number M is ам where
ao
VI – M2
Provided the Mach number does not exceed about 0.75 as stated above, the effect of compressibility on the section drag is very small. If the Mach number of any part of the blade exceeds the value given above, although the exact value depends on the profile and thickness/chord ratio of the blade section, that part of the blade loses lift while its drag rises sharply, leading to a very marked loss in overall efficiency and increase in noise.
Example 9.5 At 1.25m radius on a 4-bladed airscrew of 3.5m diameter the local chord of each of the blades is 250 mm and the geometric pitch is 4.4 m. The lift-curve slope of the blade section in incompressible flow is 0.1 per degree, and the lift/drag ratio may, as an approximation, be taken to be constant at 50. Estimate the thrust and torque gradings and the local efficiency in flight at 4600m (cr = 0.629, temperature = —14.7°С), at a flight speed of 67ms-1 TAS and a rotational speed of 1500rpm.
The solution of this problem is essentially a process of successive approximation to the values of a and b.
Be 4×0.25
solidity a = -— = ——— —r-r = 0.1273
2 2-кг 27ГХІ.25
1500 rpm = 25rps = n
 |
|
tan7 = — whence 7=1.15°
Suitable values for initial guesses for a and b are a = 0.1, b = 0.02. Then
итф = 0.3418^ = 0.383 и. Уо
ф = 20.93°, a = 29.3 – 20.93 = 8.37° Kr V(l +a) cosec ф
![]() V(l + a) _ 67 x 1.1 sin<£ 0.357
V(l + a) _ 67 x 1.1 sin<£ 0.357
M = ^ = 0-635, Vl-M2 = 0.773
= = °’1295 Per degree
da 0.773
Since a is the absolute incidence, i. e. the incidence from zero lift:
CL = a^ = 0.1295 x 8.37 = 1.083 da
Then
q= Cz, sin(0 + 7) = 1.083 sin(20.93 + 1.15)° =0.408
t = Cz, cos(0 + 7) = 1.083 cos 22.08° = 1.004
giving
, 0.0384 „
b = – = 0.0371
1.0384
a 1 2j 0.1274x 1.004
—— = – at cosecІф = -—_ — = 0.2515
1 + a 4 Y 4 x 0.357 x 0.357
giving
![]() 0.2515 л a= ,-=0.336
0.2515 л a= ,-=0.336
Thus the assumed values a = 0.1 and b = 0.02 lead to the better approximations a = 0.336 and b = 0.0371, and a further iteration may be made using these values of a and b. A rather quicker approach to the final values of a and b may be made by using, as the initial values for an iteration, the arithmetic mean of the input and output values of the previous iteration. Thus, in the present example, the values for the next iteration would be a = 0.218 and b = 0.0286. The use of the arithmetic mean is particularly convenient when giving instructions to computers (whether human or electronic).
The iteration process is continued until agreement to the desired accuracy is obtained between the assumed and derived values of a and b. The results of the iterations were:
a = 0.1950 b = 0.0296
to four significant figures. With these values for a and b substituted in the appropriate equations, the following results are obtained:
ф = 22°48′ a = 6°28′
KR = 207 ms-‘ M = 0.640
giving
= i;pVlcl = 3167Nm 1 per blade dr 2 K
and
= ^pV^crq = 1758 N mm 1 per blade
Thus the thrust grading for the whole airscrew is 12 670Nm_1 and the torque grading is 7032 N mm-1.
The local efficiency is
– = 0.768 or 76.8%
2nnr q











