The Wlam1 method

The task of deciding the pressure altitude required to establish a desired referred weight is complicated in this case by the additional requirement to account for the prevailing air temperature profile. Since this profile can only be estimated prior to flight, any planning tool can only be used to predict the required altitude. A final check on the actual referred weight at the instant the test conditions are established will be required. Suppose that the test aircraft has a standard rotor speed of )0 and that data is required at some other rotor speed ()). The relative rotor speed (m) is therefore obtained from:

m =

Now suppose that a test flight is to be conducted using a take-off weight of WTO and that data is required at a referred weight (W/am2) of WREF. At any point in the sortie, if the fuel burn is WFUEL then the relative density required for the desired W/am2 is given by:

( WTO ~ WFUEL)
WREF m2

Given an estimate of the temperature profile it is possible to determine the pressure altitude at which the required relative density is likely to occur. Test planning using this concept is more readily achieved by graphical means. The relative density at any pressure altitude is obtained from standard atmospheric equations and compared with that required for the test point(s). The atmospheric equations are:

5 = (1 – 6.8756 X 10 -6Hp) 5-2 5 59

h T + 273.15
= 288.15

5

a = 0

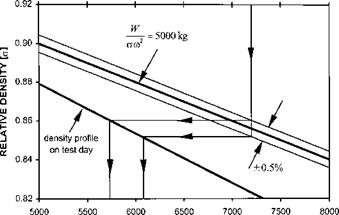
Figure 3.3 shows how test requirements can be plotted for ease of pre-flight planning. The example shows the pressure altitude range for the desired referred weight +0.5%.

The style of planning chart shown in Fig. 3.3 has been successfully used to test helicopters with fixed rotor speed () = )0 at all times) as well as those that feature a ground adjustable datum rotor speed. It cannot be used, however, if the test requires maintenance of m/^9 as well as W/am2 since in adjusting the rotor speed to set m/^9 the referred weight will be altered. The requirement to obtain performance information at constant m/^9 and W/am2 occurs quite often, especially during the evaluation of tip effects (TE). In these situations an alternative approach is required. As mentioned earlier, if the test team can adjust the rotor speed in flight then the W/8 method may be used. Noting the relationship between W/8 and W/am2 gives the alternative method:

W (_mY = _W = W

am2 X y^9J a9 8

Therefore, the desired value of Wlam2 can be converted into a target value of W/8. Provided this value can be obtained and the rotor speed can be adjusted to generate the desired m/^9 at the test altitude then the required value of W/am2 can be tested indirectly.