Analysis of Climbs and Autorotafion by the Energy Method
Energy methods based on the power required in level flight are useful for making first approximations of the extra power required to climb or the rate of descent in
|
ZJD
Forward Speed, knots |
|
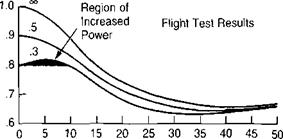
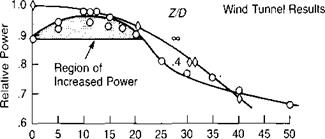
Forward Speed, knots FIGURE 3.11 Experimental Evidence of Ground Effect |
Sources: Cheesman & Bennett, “The Effect of the Ground on a Helicopter Rotor in Forward Flight,” British R&M 3021, 1957; Sheridan & Wiesner, “Aerodynamics of Helicopter Flight Near the Ground,” AHS 33rd Forum, 1977.
autorotation. For more exact calculations, the methods outlined in the section on use of the charts later in this chapter should be used.
The extra power required to climb compared to that required to fly level may be estimated from the rate of change in potential energy. For a rate of climb, R/C, in ft/min:
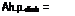
(R/C)(GM.)
33,000
For the example helicopter this approach gives a first approximation:
Ah. p.dimb = Q.6l(R/C)
The best rate of climb will be achieved at the speed for which the power required for level flight is a minimum, since at this speed the A h. p. available from
the engine will be a maximum. Figure 3.8 shows that for the example helicopter this speed is about 75 knots.
In autorotation, the same approach may be used; that is, the rate of change of potential energy must be large enough to supply power equal to that required for level flight:
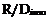 33,000 h. p.
33,000 h. p.
G. W.
The minimum rate of descent also is achieved at the speed for minimum power required in level flight. The effect of several significant parameters on the autorotative rate of descent can be seen by writing the power-required equation as:
Thus:
The effect of varying disc loading, equivalent flat plate area, and gross weight on the autorotative rate of descent of the example helicopter at 75 knots is shown below. (The profile power is assumed to remain constant).
|
Case Parameter |
One |
Two |
Three |
Four |
Five |
|
Disc loading, D. L. |
7.1 |
3.55 |
7.1 |
3.55 |
7.1 |
|
Equiv. flat plate area,/ ft2 |
19.3 |
19.3 |
19.3 |
19.3 |
9.65 |
|
Gross weight, G. W. |
20,000 |
20,000 |
10,000 |
10,000 |
20,000 |
|
h. p., level flight |
. 1,070 |
780 |
780 |
635 |
1,025 |
|
K/DAuto> ft/min |
1,765 |
1,295 |
2,580 |
2,100 |
1,690 |
Comparing cases 1 and 4 leads to the somewhat surprising conclusion that the lighter a helicopter, the faster its autorotative rate of descent. This paradox can be explained by comparing the total potential energy at the two weights and the power required to fly in level flight. The potential energy is only half as much in case 4 as in case 1, but the power required is more than half as high. To obtain this power from the loss in potential energy, the lighter helicopter must come down faster.
Figure 3.13 shows results obtained during flight tests of the Lockheed Model 286 helicopter. The decrease in rate of descent with increasing gross weight
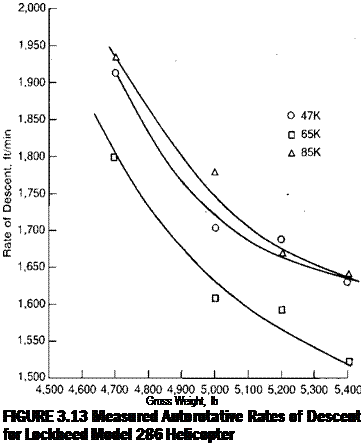 |
Source: Internal Lockheed report.
is evident. The trend would be expected to hold only until the rotor was so heavily loaded that blade stall- would cause the profile power to increase rapidly.