Angular Momentum of Rigid Bodies

In most of our applications, the collection of particles can be assumed mutu­ally fixed. This idealization, called a rigid body, is physically not realistic because molecules, even in solid matter, are oscillating. However, our macroscopic perspec­tive permits this simplification. We need to be careful only when bending and vibra­tions (flutter) di stort the airframe to such an extent that aerodynamic and mass prop­erties are significantly changed. Here, we take advantage of the rigid-body concept.

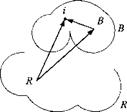
Theorem: The angular momentum lHRR of a rigid body В wrt to any reference

frame R and referred to reference point R can be calculated from two additive terms:

If = IBBLJBR + mBSBRvR (6.18)

The first term is the angular momentum l^R of body В wrt to reference frame R and referred to its own c. m. B, lBR = Івшвк, and the second term is a transfer factor accounting for the fact that R is not the c. m. Replacing the linear velocity by its definition Vj – DRsBR results in another useful formulation:

Ir — і ВШ +W ^brU SBR (6.19)

Proof: From Fig. 6.8 we derive the vector triangle and then take the rotational derivative wrt the reference frame R:

Fig. 6.8 Center of mass.

Substitute both into Eq. (6.17):

1Brs = + SBR){DRsm + Z7sSbr)]

Before we multiply out the terms, we use the Euler transformation to shift the rotational derivative of DRs, n to the В frame DRsiB — DBsiB + flBRsiB and take advantage of the rigid-body assumption, i. e., DBsiB = 0 (all particles are fixed wrt the c. m.):

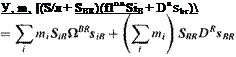iBR

lR

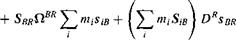(6.20)

The last two terms vanish because В is the c. m. The first term on the right-hand side is modified by first reversing the vector product and then transposing it to remove the negative sign:

У^ miSiBilBRsiB = – У^ miSiBSiBu>BR = У"’ mjSiBSiB<jjBR (6.21)

І І І

Eureka, we have unearthed the MOI tensor £]. ntiSiBSlB = /1 [see Eq. (6.1)]! The first term therefore becomes

(6.22)

The second term of Eq. (6.20) is simply

Substituting these terms into Eq. (6.20) yields

and proves the theorem.

The angular momentum of Eq. (6.18) consists of a rotary part Ibujbr with the angular velocity uiBR of the body wrt the reference frame and a transfer term mBSfiRvfj with all mass concentrated at the c. m. If the reference point is the c. m. itself, SBb — 0, and the transfer term vanishes:

І в =Івш (6.23)

Because the displacement vector sbr is not part of the calculations any longer, the angular momentum has become independent of the translational motion v B of the body’s mass center. What a welcome simplification! The c. m. as reference point separates the translational dynamics from the attitude motions.

Example 6.5 Change of Reference Frame

Problem. Suppose the angular momentum lBB’ of vehicle В wrt the J2000 inertial frame I and referred to the vehicle’s c. m. В is known only wrt the Earth frame E, i. e., lBnE. What is the error if we neglect the difference?

Solution. Expand the angular velocity uinl — uiBE + uiEI and substitute it into Eq. (6.23):

lBI _ jB BE, jB El lB — ІВШ + 1 ВШ

The first term on the right-hand side is I%ojbe — lBBE, and therefore the error is

tb, ,ei lBu> .

Do you appreciate now the significance of the MOI? Because it is a second – order tensor, it acts like a transformation that converts the angular velocity vector into the angular momentum vector. However, the MOI being a symmetrical tensor alters not only the direction but also the magnitude of uiBR.